Back to the basics with BASIC (and Python): Binary Search
By Michael Doornbos
- 7 minutes read - 1421 wordsBack to the basics with basic
Let’s say for a moment that we’ve got an ordered list of numbers.
1,3,5,7,9,11,13,15,17,19,21,23,25
There are 13 values here and we want to check if the number 25 is in this list.
One way to do this would be to loop over each element in the list and check to see if it matches what we’re looking for.
In BASIC, we’d do something like
20 FOR I=1 TO LEN(A)
30 IF A(I) = 25
This is called a linear search. You’ll also sometimes hear it called a sequential or simple search.
How many loops would it take to find out if it’s in the list?
Since it’s the last value of the list/array, which has a length of 13, it will take 13 loops before we get to it.
What if we had a list of 1,000,000 numbers? It would take 1,000,000 loops to find out if the number is in the list. That’s a lot of loops.
Computer scientists have a notation for this: Big O notation. It’s a way to describe the performance of an algorithm. In this case, the linear search is
$$O(n)$$Because the number of loops is directly proportional to the number of elements in the list.
What if we could search 1,000,000 in less than 50 loops? That would be great, right?
Let’s get back to our list:
1,3,5,7,9,11,13,15,17,19,21,23,25
This only works on ordered lists. We’ll tackle sorting lists in a later post.
Let’s use a binary search to find the number 25 in the list.
We start by looking at the middle value of the list. In this case, it’s 13. We compare 13 to 25. Since 13 is less than 25, we know that 25 is not in the first half of the list. We can ignore the first half of the list and look at the second half.
15,17,19,21,23,25
We repeat the process. We look at the middle value of the list. In this case, it’s 19. We compare 19 to 25. Since 19 is less than 25, we know that 25 is not in the first half of the list. We can ignore the first half of the list and look at the second half.
21,23,25
And again, we look at the middle value of the list. In this case, it’s 23. Since 23 is less than 25, we know that 25 is not in the first half of the list. We are left with:
25
And there it is. We found it in 3 loops.
Binary search has a Big O notation as well; it happens to work out to about
$$O(\log_2 n)$$Obviously, this will be much faster than a linear search.
How much faster? Let’s do a little experiment.
Binary vs Linear Search in Commodore 64 BASIC
5 TI$="000000":PRINTCHR$(147)
10 PRINT" BINARY VS LINEAR SEARCH IN BASIC":PRINT:PRINT
20 LE=7500:DIM A(LE):C=1:CT=0
30 FORI=1TOLE:A(I)=C:C=C+2:NEXT
35 PRINT"SETUP ";:GOSUB200:PRINT
40 PRINT "ENTER SEARCH VALUE";:INPUT V
43 REM BINARY SEARCH =================
45 TI$="000000"
47 PRINT:PRINT"BINARY SEARCH FOR"V"IN"LE"RECORDS"
50 L=1:H=LE:REM LOW, HIGH
60 IF L> HTHENPRINT"NOT FOUND":PRINT"TOTAL LOOPS:"CT:GOSUB200:GOTO100
65 CT=CT+1
70 M=INT((L+H)/2):REM MID POINT
80 IF A(M)=VTHENPRINT"FOUND AT"M:PRINT"TOTAL LOOPS:"CT:GOSUB200:GOTO100
90 IF A(M)>V THEN H=M-1:GOTO60
95 IF A(M)<V THEN L=M+1:GOTO60
100 REM LINEAR SEARCH ================
105 PRINT:?:?"LINEAR SEARCH FOR"V"IN"LE"RECORDS"
110 TI$="000000":C=1:CT=0
120 FORI=1TOLE
130 CT=CT+1
140 IF A(I)=VTHENPRINT"FOUND AT"M:PRINT"TOTAL LOOPS:"CT:GOSUB200:END
150 NEXT
160 PRINT"NOT FOUND":PRINT"TOTAL LOOPS:"CT:GOSUB200:END
200 REM TIME =========================
210 PRINT"TOOK"TI/60"SECONDS"
220 RETURN
Here, we’re searching for the last element in a list of 15,000 numbers to see how many loops it takes to find it. I picked the last element in the list/array to make the linear search take the maximum amount of time for this list/array.
Let’s break it down:
Initialization
- Line 20 initializes an array
Awith 7500 elements (LE=7500).C=1initializes the counter for the array values, andCT=0is for counting the number of loops or iterations in the searches.
Array Setup
- Lines 30-30 populate the array
Awith odd numbers starting from 1 (sinceCstarts at 1 and is incremented by 2 in every loop). I intentionally set this up with odd numbers so we can know the values we’re searching for ahead of time to make the demonstration easier.
Binary Search
- Lines 45-95 implement the binary search algorithm. We repeatedly divided in half the portion of the list that could contain the target value, thereby reducing the search area by half each time. The variables
LandHrepresent the current low and high bounds of the search area within the array. The mid-pointMis calculated, and depending on comparing the value atA(M)with the target valueV,the search area is adjusted. The process repeats until the value is found or the search area is reduced to zero. The number of loops taken to see the value or conclude it’s not present is counted withCT.
Linear Search
- Lines 105-160 implement the linear search algorithm, which goes through each element of the array
Afrom the beginning to the end, looking for the valueV.The search stops if the value is found, with the number of loops recorded inCT.
Commodore 64 Results
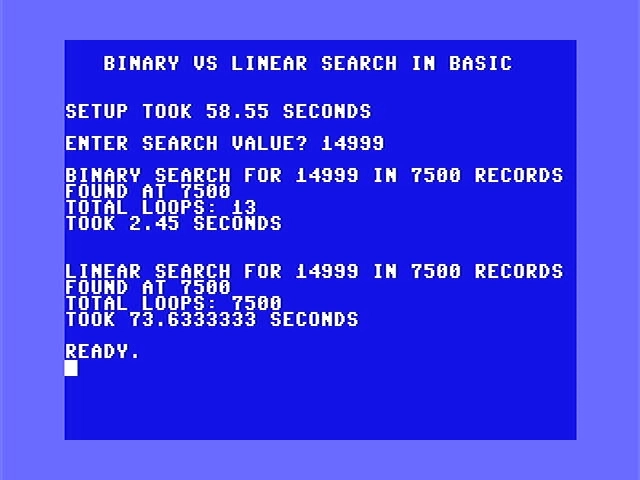
How does this translate to modern programming?
That’s great, but a modern computer can search through 7500 records in a fraction of a second. How does this apply to modern programming?
Let’s take a look at a Python implementation of the same algorithm and give it a much larger list to search through. I think you’ll find the results interesting.
import time
import numpy as np
# Decorator to measure the execution time of functions and return execution time
def timeit(func):
def wrapper(*args, **kwargs):
start_time = time.perf_counter()
result = func(*args, **kwargs)
elapsed_time = time.perf_counter() - start_time
# Return both the result and the elapsed time
return result, elapsed_time
return wrapper
@timeit
def binary_search(arr, value):
low = 0
high = len(arr) - 1
loops = 0
while low <= high:
loops += 1
mid = (low + high) // 2
if arr[mid] == value:
return mid, loops
elif arr[mid] < value:
low = mid + 1
else:
high = mid - 1
return None, loops
@timeit
def linear_search(arr, value):
loops = 0
for i, val in enumerate(arr):
loops += 1
if val == value:
return i, loops
return None, loops
def setup_array(length):
return np.arange(1, length*2, 2)
# Main program starts here
if __name__ == "__main__":
print("\n BINARY VS LINEAR SEARCH IN PYTHON\n")
length = 750_000_000
arr = setup_array(length)
value = int(input("ENTER SEARCH VALUE: "))
#value = length*2 - 1
# Perform Binary Search
(result, loops), elapsed_time = binary_search(arr, value)
if result is not None:
print(f"\nBINARY SEARCH FOR {value} IN {length} RECORDS")
print(f"FOUND AT {result}. TOTAL LOOPS: {loops}")
else:
print("NOT FOUND")
print(f"TOOK {elapsed_time:.6f} SECONDS")
# Perform Linear Search
(result, loops), elapsed_time = linear_search(arr, value)
if result is not None:
print(f"\nLINEAR SEARCH FOR {value} IN {length} RECORDS")
print(f"FOUND AT {result}. TOTAL LOOPS: {loops}")
else:
print("NOT FOUND")
print(f"TOOK {elapsed_time:.6f} SECONDS")
Python Results
BINARY VS LINEAR SEARCH IN PYTHON
ENTER SEARCH VALUE: 1499999999
BINARY SEARCH FOR 1499999999 IN 750000000 RECORDS
FOUND AT 749999999. TOTAL LOOPS: 30
TOOK 0.000348 SECONDS
LINEAR SEARCH FOR 1499999999 IN 750000000 RECORDS
FOUND AT 749999999. TOTAL LOOPS: 750000000
TOOK 117.734513 SECONDS
We could make this faster in several ways, but this implementation is good enough for our purposes and easy to understand. It also closely duplicates the functionality of the Commodore 64 BASIC program.
The results are fun.
We can calculate the percentage of time saved by using the binary search over the linear search.
$$\text{Percentage Change} = \left( \frac{V_{\text{final}} - V_{\text{initial}}}{V_{\text{initial}}} \right) \times 100$$So, if we plug in the values for the Python implementation:
$$ \text{Percentage Change} = \left( \frac{133.885119 - 0.001056}{0.001056} \right) \times 100 = 12,678,415.06\% $$It’s only, you know… 12 million pecent faster. No big deal ;-)
The Commodore version is:
$$ \text{Percentage Change} = \left( \frac{73.633333 - 2.45}{2.45} \right) \times 100 = 2905.4421\% $$This shows nicely how much faster the binary search is over the linear search and how the algorithm scales with the size of the list/array.
Extra credit
Try this in other programming languages and platforms. I’m going to do this in 6502 Assembly for the Commodore 64. I’ll post the results in a future article.
Conclusion
The binary search algorithm is a great example of how a simple algorithm can be much more efficient than a more straightforward approach. It’s also a great example of how a simple algorithm can be implemented in different programming languages and platforms.
Plus, a 12 million percent speed increase is fantastic.
Happy coding!
- C64
- Code
- Commodore
- Getting Started
- How-To
- Retro
- Programming
- Python
- Search
- Tutorial
- Vintage
- BASIC
- Binary Search
- Linear Search