A gentle introduction to two's complement

By Michael Doornbos

November 21, 2023 - 12 minutes read - 2359 words

I was recently on a video call with a friend, throwing around some ideas for a new product. I mentioned adding large signed numbers in assembly and using two’s complement. He asked me what two’s complement was. I was a little surprised that he didn’t know. He’s been a Java programmer for more than 30 years. Java and Python programmers (and others like gasp Commodore / MicroSoft BASIC) don’t have a native unsigned integer type. The language takes care of the details for you.

This is all fine, but the computer you’re running works with these integers internally in a simple way. It’s good to know how it works.

Plus, it’s science.

Let’s dive into it.

What is two’s complement?

Two’s complement is a system for representing signed integers that allows for straightforward binary arithmetic. To find the two’s complement of a binary number, you invert all the bits (changing 0s to 1s and 1s to 0s) and then add one to the result. This representation simplifies computer design by enabling addition and subtraction with the same circuitry, as subtracting a number is equivalent to adding its two’s complement. Additionally, it efficiently handles sign changes and zero values, which is why it’s still widely used in computing today.

Let’s do some 8-bit integer work

Note: I assume you already know how binary works. If not, here’s a good primer. Also, bitwise operations are a prerequisite for this article. If you need to get more familiar with them, here’s a good primer.

Let’s start with a simple example. We’ll use 8-bit integers because they’re easy to work with.

5 in binary is 00000101

How do we represent -5 in binary? Two’s complement uses the high bit (the one on the far left) as the sign bit. If the high bit is zero, the number is positive. If the high bit is one, the number is negative.

To find the two’s complement of 5, we invert all the bits (changing 0s to 1s and 1s to 0s) and then add one to the result.

Inverting all the bits of 00000101 gives us 11111010

Adding one to 11111010 gives us 11111011

11111011 is the two’s complement of 00000101

The decimal value of 11111011 is -5

Let’s do another just to make sure we’ve got it.

100 in binary is 01100100

Inverting all the bits of 01100100 gives us 10011011

Adding one to 10011011 gives us 10011100

10011100 is the two’s complement of 01100100

The decimal value of 10011100 is -100

Notice the high bit (the one on the far left) is zero for positive numbers and one for negative numbers. This is the sign bit.

Easy right?

By using the high bit as the sign bit, we can only represent 8-bit numbers from -128 to 127. This is because the high bit is the 128s place. If it’s zero, the number is positive.

Update 2023-11-23 User dperrin on Hacker News thinks of it like this which you might find helpful:

“When I first learned two’s complement I sort of accepted it as something to memorise for a test and didn’t really understand (or care) why it worked.

What really made it click for me was thinking of it as modular arithmetic. If you consider 8-bit integers, they range from 0-255 and you’re actually working modulo 256. So you can think of 0-127 as your non-negative numbers. The numbers from 128-255 behave as negatives modulo 256 (e.g. -1 mod 256 = 255).”

A circuit that does this

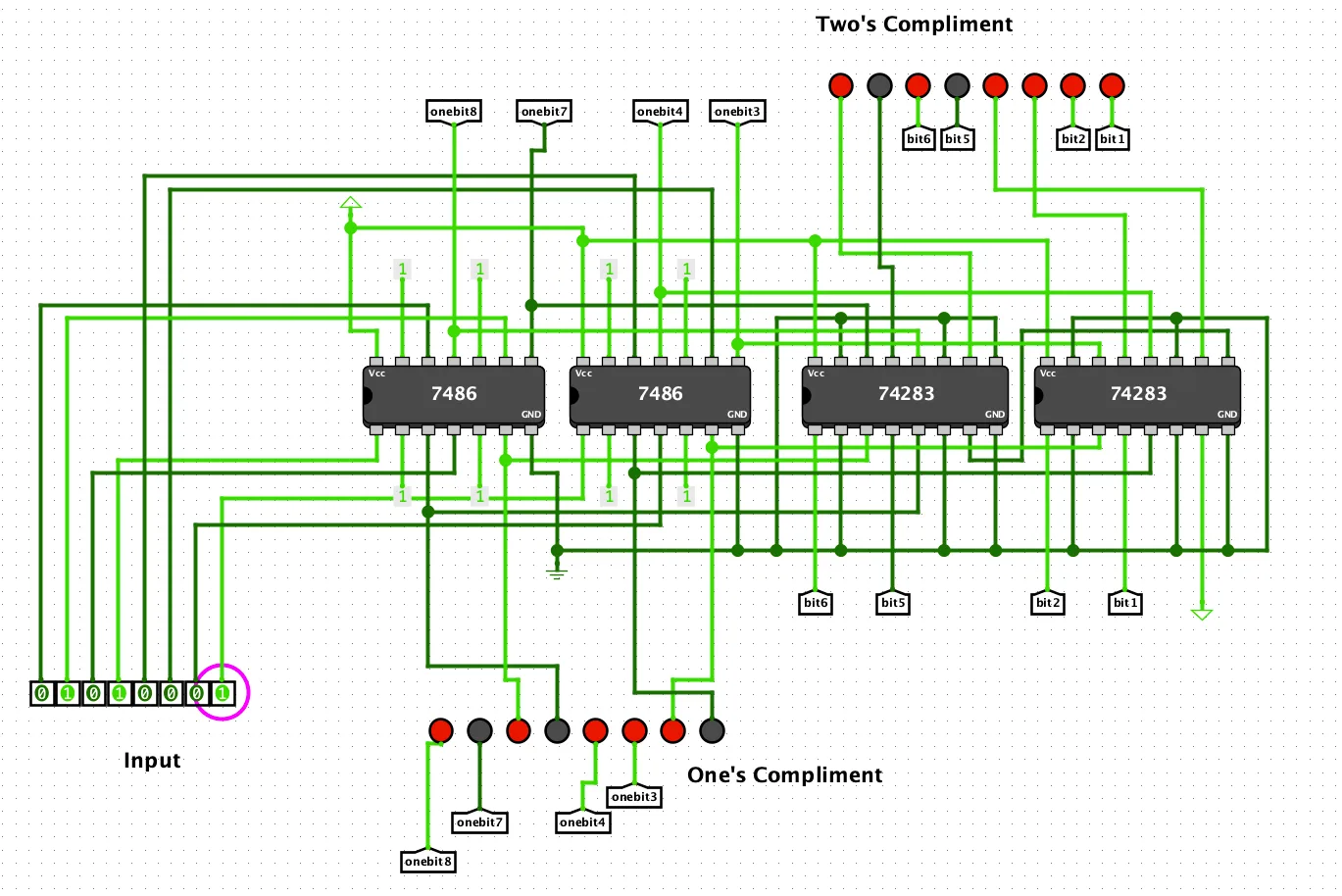
One common way to implement two’s complement is with a circuit that takes an 8-bit input and outputs its two’s complement. This circuit is composed of two parts: an inverter and an adder. The inverter takes the input and inverts all the bits, changing 0s to 1s and 1s to 0s. The adder adds one to the result, equivalent to adding the two’s complement of the input.

We can use some off-the-shelf logic gates to do this. If we want to invert a bit, using an XOR gate is the easiest way to do that. The 74LS86 chips each have 4 XOR gates. We can use two of them to invert the bits.

By the way, if you just read the bits off the gates of the 74LS86s, you’d have the one’s complement of the input. See below for more on that.

In addition, we’ll use two 74LS283 4-bit adders. We need to connect the first adder’s carry-out to the second adder’s carry-in.

Two’s complement Circuit

I used a red LED to differentiate the high bit as the sign bit.

Here’s a video of it in action, showing the two’s complement of 5 and 100 with a calculator to verify the results:

Side quest - one’s complement?

One’s complement is a system for representing signed integers similar to two’s, but it has some key differences. To find the one’s complement of a binary number, you invert all the bits (changing 0s to 1s and 1s to 0s).

Famously used in the Apollo Guidance Computer, the one’s complement system was used in early computers because it requires less hardware than two’s complement. Looking at our circuit, we can eliminate the adder and its associated wiring and use the XOR gates to invert the bits. This is the one’s complement of the input.

Logisim Circuit

However, there is a serious drawback to this system. There are two representations of zero, +0 and -0. This can lead to errors in arithmetic operations. For example, if you add +0 and -0, you get -0. Brain hurt yet?

This is not the case with two’s complement, where there is only one representation of zero.

The advantage of one’s complement (besides programmer torture) is that it’s straightforward to implement in hardware. You just invert the bits.

On our little breadboard here, you can eliminate the two chips on the right and all those wires connecting the XOR chips to the adders. Read the bits off of the XOR chips and you have the one’s complement of the input.

One’s Complement Circuit

How do I use it?

For the most part, your language takes care of this for you. The representation is internal. Some languages, like C/C++, Rust, or Swift, have signed and unsigned types, and some, like Java, Ruby, and Python, don’t.

Low-Level Languages

When using low-level languages with both unsigned and signed types, you may not know that you’re doing two’s complement; the concept is familiar even if you don’t know what is happening inside the processor.

C

#include <stdio.h>
#include <stdint.h>

int main() {
    // 8-bit unsigned integer
    uint8_t unsignedEightBit = 255; // Maximum value for 8-bit unsigned
    printf("Unsigned 8-bit value: %u\n", unsignedEightBit);

    // 8-bit signed integer
    int8_t signedEightBit = 127; // Maximum value for 8-bit signed
    printf("Signed 8-bit value: %d\n", signedEightBit);

    // Showing overflow behavior
    unsignedEightBit = 256; // This will overflow
    printf("Overflowed Unsigned 8-bit value: %u\n", unsignedEightBit);

    signedEightBit = 128; // This will overflow
    printf("Overflowed Signed 8-bit value: %d\n", signedEightBit);

    return 0;
}

uint8_t is used for the 8-bit unsigned integer. It can hold values from 0 to 255.
int8_t is used for the 8-bit signed integer. It can hold values from -128 to 127.

It is helpful to demonstrate an overflow condition here. When you assign a value too large for the type, it overflows. This overflow wraps around to zero for unsigned types, while for signed types, the behavior is technically undefined in C but often wraps similarly.

Rust

In Rust, you can use u8 for an 8-bit unsigned integer and i8 for an 8-bit signed integer. Rust provides a rich type system and safety features, including checks for integer overflow in debug builds. Here’s an example demonstrating both types in Rust:

fn main() {
    // 8-bit unsigned integer
    let unsigned_eight_bit: u8 = 255; // Maximum value for 8-bit unsigned
    println!("Unsigned 8-bit value: {}", unsigned_eight_bit);

    // 8-bit signed integer
    let signed_eight_bit: i8 = 127; // Maximum value for 8-bit signed
    println!("Signed 8-bit value: {}", signed_eight_bit);

    // Demonstrating overflow behavior
    // Note: Rust will panic in debug mode if overflow occurs.
    // To handle overflow, you can use wrapping_add, saturating_add, etc.
    let overflowed_unsigned = unsigned_eight_bit.wrapping_add(1);
    println!("Overflowed Unsigned 8-bit value: {}", overflowed_unsigned);

    let overflowed_signed = signed_eight_bit.wrapping_add(1);
    println!("Overflowed Signed 8-bit value: {}", overflowed_signed);
}

In this example:

u8 is used for the 8-bit unsigned integer, which can hold values from 0 to 255.
i8 is used for the 8-bit signed integer, which can hold values from -128 to 127.

The overflow behavior in Rust differs from C. By default, Rust checks for overflow in debug builds and will panic if an overflow is detected. Overflow checks are not included for performance reasons for release builds, and the behavior is similar to C (wrapping around). However, Rust provides methods like wrapping_add and saturating_add to handle overflows explicitly and safely.

How do I do it in assembly?

I still like to teach 6502 assembly as a first assembly language. It’s simple and a great way to learn about how computers work. It’s also a great way to learn about two’s complement because we’re limited to 8-bit values inside the processor. So, we can embrace this constraint to grasp the concept.

Plus, you’re on this site. What were you expecting?

6502 Assembly

In 6502 assembly language, the concept of signed and unsigned integers is not explicitly defined by the data types, as in higher-level languages. Instead, it’s more about how you interpret and manipulate the data in your assembly code. The 6502 processor works with 8-bit data and 16-bit addresses.

Here’s a basic example to illustrate handling signed and unsigned 8-bit values in 6502 assembly:

    LDA #$FF       ; Load the accumulator with an 8-bit value (255 in decimal, or -1 if interpreted as signed)
    STA $0200      ; Store the value in memory location $0200

    LDA #$7F       ; Load the accumulator with 127 (the maximum positive value for a signed 8-bit number)
    STA $0201      ; Store the value in memory location $0201

The LDA #$FF instruction loads the accumulator with 0xFF (255 in decimal). If you interpret this as an unsigned byte, it’s 255. If you interpret it as a signed byte (using two’s complement), it’s -1.
The LDA #$7F instruction loads the accumulator with 0x7F (127 in decimal), which is the maximum value for a signed 8-bit integer in two’s complement representation.

The 6502 processor doesn’t distinguish between signed and unsigned numbers. It’s up to the programmer to use the appropriate instructions for the intended interpretation.

For example, the BPL (Branch if PLus) and BMI (Branch if MInus) instructions can be used to branch based on whether the most recent operation resulted in a positive or negative signed number, while other instructions like BCS (Branch if Carry Set) and BCC (Branch if Carry Clear) are used for unsigned comparisons.

It is like driving a manual transmission car. The car doesn’t care if you’re going forward or backward; using the right gear is up to you. And if you use the right gear, you will have a good time. But those who drive manual transmissions know it’s worth it. Sometimes.

If you don’t have access to a 6502 based computer you can use an emulator or an online assembler. I like this one.

Commodore BASIC Chart

Commodore BASIC handles signed and unsigned integers for you. But I can’t have an article on this site without a vintage computer, can I?

THINK OF THE CHILDREN!!

Here on the Commodore 128 (this should work on many early 80s dialects of BASIC), we can see how this works:


2 PRINTCHR$(147)
3 PRINT"TWOS COMPLEMENT CHART FOR 8 BIT VALUES"
4 PRINT"----------------------------------------"
5 PRINT"POSITIVE  NEGATIVE   UNSIGNED BINARY"
10 FOR N=0TO127
30 T=0
40 FOR I=0 TO 7
50 B=2^I
60 IF (N AND B) = B THEN GOTO80
70 T=T+B
80 NEXT I
90 T=(T+1) AND 255
100 PRINT N,-N,T,
120 FOR I=7 TO 0 STEP -1
130 B=2^I
140 IF (T AND B) = B THEN PRINT "1";:GOTO 150
145 PRINT "0";
150 NEXT I
160 PRINT
170 NEXT

Interestingly, the Commodore documentation for AND calls it a logical AND. But you can use it to check if bits are set, so it IS bitwise AND in the right hands.

Logical AND vs Bitwise AND

FPGA Version

No breadboard, no problem. Just grab your pocket FPGA, and you’re good to go.

You do have an FPGA in your pocket, don’t you?

It’s easy to implement two’s complement in an FPGA. Here’s an example of a module that takes an 8-bit input and outputs its two’s complement:

module TwosComplement(
    input [7:0] in,   // 8-bit input
    output [7:0] out  // 8-bit output representing the two's complement
);

// Inverting all bits of the input, equivalent to our 74LS86 XOR gates
wire [7:0] inverted;
assign inverted = ~in;

// Adding 1 to the inverted input, equivalent to our 74LS283 adders
assign out = inverted + 1;

endmodule

Since the registers are 8-bit wide, these will wrap around and work for all 8-bit integers. Like assembly, the FPGA doesn’t care if it’s signed or unsigned; it’s up to you to use the correct interpretation—vroom vroom.

You can also just grab that inverted signal if you wanted to try working with one’s complement.

The HP-16C

HP-16C

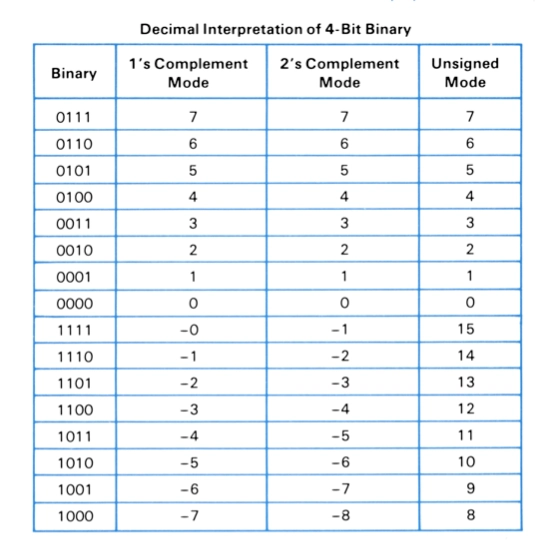
The HP-16C programmable calculator supports one’s and two’s complements. It’s weird and quirky, but I love it.

There is a great chart from the HP-16C manual that shows the one’s and two’s complements of all of the 4-bit integers. I found it very helpful when I was learning about this years ago.

HP-16C User Manual Chart

Was this gentle?

Was this gentle? I hope so. If you have questions, please let me know.