My friend Robin’s favorite demo is 10 print. And what’s not to love about 10 print? After all, there’s even a book about it.

My Favorite Demo

My favorite demo is more complex but still simple enough to understand. The Maze Generator, from Compute! December 1981 by Charles Bond has been a favorite of mine since it came out. In the filing cabinet of my mind, I even remember it as the “Page 54 Maze”.

The magazine has PET and Atari BASIC versions that you can compare to each other. Who doesn’t like a good race between old computery things?

Compute’s First Book of Games

Charles Bond continued this work in Compute’s First Book of C64 Games with the original program (C64 version, which is the same with the screen location changed from 32768 to 1024) and a Machine Language program. It’s an excellent adaptation of the original; as expected, it’s dramatically faster than the BASIC version.

While there is an Assembly listing, there isn’t much explanation of the Assembly code, what it’s doing, and how it relates to the BASIC version. We’ll tackle that in part two. Today, we’re going to go over how the BASIC version works.

How this algorithm works

BASIC Version

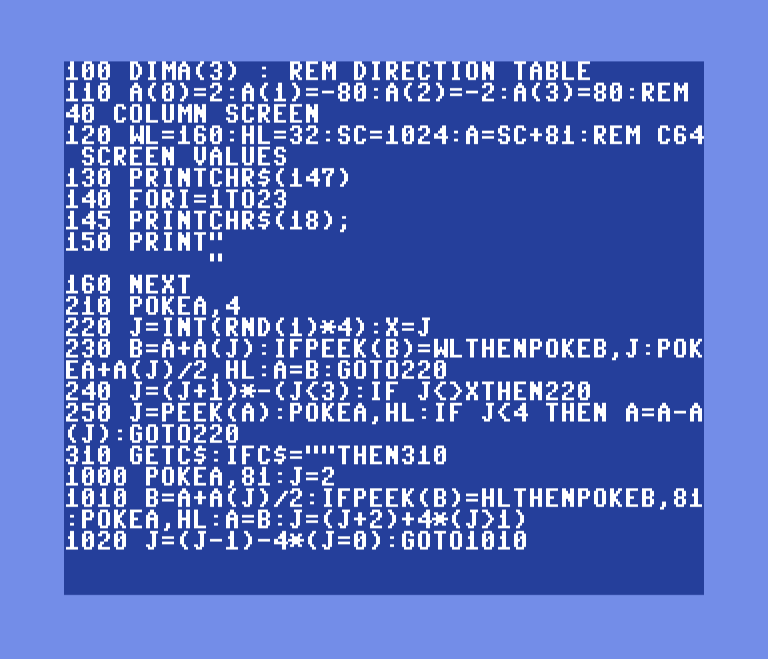Elegant and fits on a single screen

The First Book of Commodore 64 Games book does break down this program. Let’s go over that, but line by line.

    100 DIMA(3)
    110 A(0)=2:A(1)=-80:A(2)=-2:A(3)=80

Lines 100 and 110, we set up a simple array that gives us East, North, West, and South movements.

    120 WL=160:HL=32:SC=1024:A=SC+81

This is the line of variables that set things up. WL is a reserved space, and HL is a space. SC is the start of screen memory. This may change depending on your machine. For example, on a Commodore PET, this will be 32768. The last variable is where the maze will start. This can be anywhere that’s a valid screen location on your machine as long as it’s an odd number. Try experimenting with this one and see what happens.

I changed line 130 to print the clear screen character for clarity and added line 145 to set the text color to white in my C64 version. Not needed on a PET, though.

    140 FORI=1TO23
    145 PRINTCHR$(18);
    150 PRINT"                                       "
    160 NEXT

Lines 140-160, we draw a reversed space, effectively filling in the screen with white spaces, leaving a border.

    210 POKEA,4

Line 210 sets a starting position.

    220 J=INT(RND(1)*4):X=J
    230 B=A+A(J):IFPEEK(B)=WLTHENPOKEB,J:POKEA+A(J)/2,HL:A=B:GOTO220
    240 J=(J+1)*-(J<3):IF J<>XTHEN220
    250 J=PEEK(A):POKEA,HL:IF J<4 THEN A=A-A(J):GOTO220

Now we’re into the magic. It’s amazing what you can do with four lines of code here.

Line 220, we pick a random direction from 1 to 4 and set X with that random value.

Line 230 this one is several parts. Let’s do them one at a time.

• Move in the random direction

• Check to see if that location is a reversed space, indicating we’ve not been here yet

• If it is, set a marker with the direction

• Set the adjoining location to a blank space

• Set the location to that adjoining location

• Go back to 220 and do it again

Line 240 Pick a direction (turn right). If it’s the direction we came from, pick a new random direction.

Line 250 Save what’s in the current position to J. Set to a space. If it’s a space, we’ve been to, move to the next location and repeat.

Visualize it

Sometimes it’s helpful to visualize what’s happening. Since the computer we’re doing this on is slow, we can follow along as the values are changed.

We’ll use a build in routine to place the cursor

Side Hustle - Other column-width screens

This needs a few changes to work on the narrower screen of a VIC-20. You can also use this example to port this to other screen sizes. Pretty easy to make this work on an 80-column machine with edits to line 110 in this spirit.

    100 DIMA(3) : REM DIRECTION TABLE
    110 A(0)=2:A(1)=-44:A(2)=-2:A(3)=44:REM 22 COLUMN SCREEN
    120 WL=160:HL=32:SC=7680:A=SC+45:REM UNEXPANDED VIC
    130 PRINTCHR$(147)
    140 FORI=1TO21
    145 PRINTCHR$(18);
    150 PRINT"                     "
    160 NEXT
    200 REM GENERATE THE MAZE
    210 POKEA,4
    220 J=INT(RND(1)*4):X=J
    230 B=A+A(J):IFPEEK(B)=WLTHENPOKEB,J:POKEA+A(J)/2,HL:A=B:GOTO220
    240 J=(J+1)*-(J<3):IF J<>XTHEN230
    250 J=PEEK(A):POKEA,HL:IF J<4 THEN A=A-A(J):GOTO220
    300 REM WAIT FOR KEYPRESS
    310 GETC$:IFC$=""THEN310
    1000 REM MAZE TRANSVERSAL PROGRAM
    1010 POKEA,81:J=2
    1020 B=A+A(J)/2:IFPEEK(B)=HLTHENPOKEB,81:POKEA,HL:A=B:J=(J+2)+4*(J>1)
    1030 J=(J-1)-4*(J=0):GOTO1020

VIC-20 Version

    100 dima(3) : rem direction table
    110 a(0)=2:a(1)=-160:a(2)=-2:a(3)=160:rem 80 column screen
    120 wl=160:hl=32:sc=32768:a=sc+161:rem PET screen values
    130 printchr$(147)
    140 fori=1to23
    145 printchr$(18);
    150 print"                                       ";
    151 print"                                        "
    160 next
    200 rem generate the maze
    210 pokea,4
    220 j=int(rnd(1)*4):x=j
    230 b=a+a(j):ifpeek(b)=wlthenpokeb,j:pokea+a(j)/2,hl:a=b:goto220
    240 j=(j+1)*-(j<3):if j<>xthen230
    250 j=peek(a):pokea,hl:if j<4 then a=a-a(j):goto220
    300 rem wait for keypress
    310 getc$:ifc$=""then310
    1000 rem maze transversal program
    1010 pokea,81:j=2
    1020 b=a+a(j)/2:ifpeek(b)=hlthenpokeb,81:pokea,hl:a=b:j=(j+2)+4*(j>1)
    1030 j=(j-1)-4*(j=0):goto1020

PET-80 Column / can be easily adapted to a Commodore 128 Version

What makes it “the best”?

It’s subjective, but I love this one because it’s powerful AND easy to understand. It runs slow enough on a 1Mhz machine to follow and see what it’s doing.

Extra credit

Lines 1000 to 1030 “traverse” the maze. Can you figure out how it works before we review it in part 2?

    1000 REM MAZE TRANSVERSAL PROGRAM
    1010 POKEA,81:J=2
    1020 B=A+A(J)/2:IFPEEK(B)=HLTHENPOKEB,81:POKEA,HL:A=B:J=(J+2)+4*(J>1)
    1030 J=(J-1)-4*(J=0):GOTO1020

• C64
• Code
• Commodore
• Crypto
• Getting Started
• How-To
• KIM-1
• PET
• Retro
• VIC-20