64 Bit Addition and Products on Commodore: The Wheat and Chessboard problem
By Michael Doornbos
- 5 minutes read - 953 wordsDealing with large numbers in computing has been an attractive problem area for a long time. Using an average calculator might lead you to believe that it’s too tricky for most applications.
But it’s not that difficult. And to prove it, we’re going to implement this calculation on machines with 8 Bit registers (I mean, cmon, on this site, you can’t even pretend to be shocked).
Big numbers with the wheat and chessboard problem
A classic math exercise is called the wheat and chessboard problem.
If a chessboard were to have wheat placed upon each square such that one grain were placed on the first square, two on the second, four on the third, and so on (doubling the number of grains on each subsequent square), how many grains of wheat would be on the chessboard at the finish?
We can do this with simple addition. As a review, the largest 32-bit integer is 2^32 or 4,294,967,296. After that many digits calculators, and even languages, default to scientific notation. Something like:
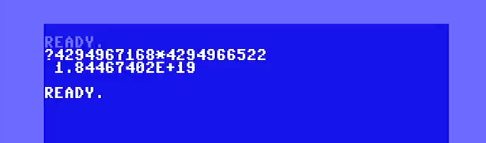
Let’s visualize what we’re going to build in assembly in an easy to read language:
grains_sum = UInt64(0)
grains = UInt64(1)
wheat_mass = 65 # assume 65 mg per "grain"
for square in range(1, 64)
grains_sum += grains
println("square $(square) grains $(grains) total $(grains_sum)")
grains *= 2
end
total_mass_kg = UInt128(fld(grains_sum * wheat_mass,1000))
println("$(total_mass_kg) kg")%
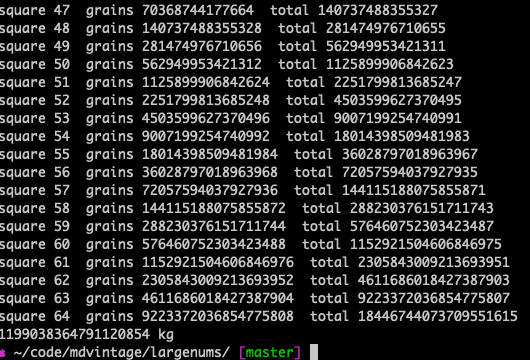
This takes just a few milliseconds.
Pretty easy. Loop 64 times, add the number of grains to the previous and double the current for the next loop.
Let’s code
You might think this would be difficult on an 8 Bit processor, but it’s not. To add two 8-bit numbers together, we simply add with carry the low byte and then do it over and over for the next 7 bytes. The carry bit moves on down with our addition. Easy peasy.
addgrains
clc
lda grainssum
adc grains
sta grainssum
lda grainssum+1
adc grains+1
sta grainssum+1
lda grainssum+2
adc grains+2
sta grainssum+2
lda grainssum+3
adc grains+3
sta grainssum+3
lda grainssum+4
adc grains+4
sta grainssum+4
lda grainssum+5
adc grains+5
sta grainssum+5
lda grainssum+6
adc grains+6
sta grainssum+6
lda grainssum+7
adc grains+7
sta grainssum+7
rts
.bend
We can certainly do this in a loop over one of the index registers to make the code shorter, but this is the same thing, and I think the concept is more clearly written this way. We’ve gone for understanding here.
Multiply
Fortunately, the problem we’ve chosen to tackle here is a multiply by two, which any computer going back to the 1960s can do pretty easily. Binary multiply and divide are just shifting left (multiply by 2) and shifting right (divide by two). Jim Butterfield’s fantastic “Machine Language for the Commodore” has an excellent set of graphics to help visualize what we’re doing here:
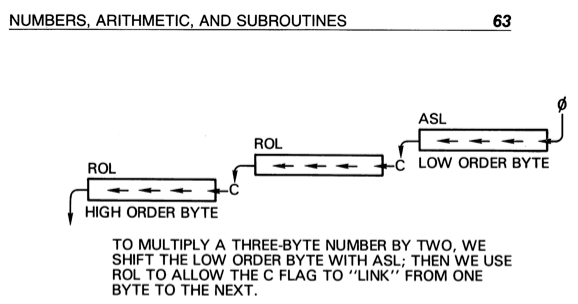
Machine Language for the Commodore Revised and Expanded Edition by Jim Butterfield
So to implement our 8-byte multiplier:
mult2grains
.block
clc
lda grains
asl a
sta grains
lda grains+1
rol a
sta grains+1
lda grains+2
rol a
sta grains+2
lda grains+3
rol a
sta grains+3
lda grains+4
rol a
sta grains+4
lda grains+5
rol a
sta grains+5
lda grains+6
rol a
sta grains+6
lda grains+7
rol a
sta grains+7
rts
.bend
We can certainly do this in a loop over one of the index registers to make the code shorter, but this is the same thing, and I think the concept is more clearly written this way. We’ve gone for understanding here. The tricky part here is actually the printing of the hex to decimal. Fortunately, we can get a head start/boost using “Graham’s” 32-bit converter on Codebase64. Such an elegant solution Graham!
printdec64
.block
jsr hex2dec
ldx #21
loop1
lda result,x
bne loop2
dex; skip leading zeros
bne loop1
loop2
lda result,x
ora #$30
jsr $ffd2
dex
bpl loop2
rts
hex2dec
ldx #0
loop3
jsr div10
sta result,x
inx
cpx #21
bne loop3
rts
div10
; divides a 64 bit value by 10
ldy #64;64 bits
lda #0
clc
loop4
rol a
cmp #10
bcc skip
sbc #10
skip
rol value
rol value+1
rol value+2
rol value+3
rol value+4
rol value+5
rol value+6
rol value+7
dey
bpl loop4
rts
.bend
We can certainly do this in a loop over one of the index registers to make the code shorter, but this is the same thing, and I think the concept is more clearly written this way. We’ve gone for understanding here. I’ve expanded Graham’s solution to work on 8 bytes (64 bits) which happens to be exactly what we need.
So how’d it turn out?
Results
VIC-20 Version is fast as you might expect, but have to give some thought on formatting this better
Finally a use for 80 column mode on a Commodore 128!
And 80 column PETs
On my KIM-1 Clone (Corsham)
Extra credit
Where do we go from here. Well, now that we can output up to 21 digits easily, we can multiply large numbers together.
mult32
.block
lda #$00
sta product
sta product+1
sta product+2
sta product+3
sta product+4
sta product+5
sta product+6
sta product+7
; set binary ct 32
ldx #$20
shiftr
lsr multiplier+3
ror multiplier+2
ror multiplier+1
;divide multiplier by 2
ror multiplier
bcc rotater
lda product+4
; get upper half of product
; and add multiplicand
clc
adc multiplicand
sta product+4
lda product+5
adc multiplicand+1
sta product+5
lda product+6
adc multiplicand+2
sta product+6
lda product+7
adc multiplicand+3
rotater
ror a ; rotate partial prod
sta product+7
ror product+6
ror product+5
ror product+4
ror product+3
ror product+2
ror product+1
ror product
dex
bne shiftr
rts
.bend
Have fun!
Sometime over the next week, I’m going to try this on the KIM-1. If you try this on another platform, please let me know!