Fibonacci 1-10 on the KIM-1 (and clones)
By Michael Doornbos
- 5 minutes read - 993 wordsSometimes there’s an absolute joy in doing something the hard way to REALLY understand what’s happening.
I struggled (still struggle) with wrapping my mind around using the display on the KIM-1. The best way (for me anyway) to be motivated to learn something is to have an outcome in mind of what I want to see and work towards that.
Most people who started on the KIM-1 probably spent a fair amount of time in an early book called “The First Book of KIM.” There are several examples of the basics in it, including one way to show memory locations on the display.
Remember I said one way, not THE way. This point will be important later…
Desired outcome
Let’s make the KIM-1 give us the first 10 entries in the Fibonacci sequence starting with 1 and display the results for a second or two each in order. Simple enough to wrap our minds around in a few minutes and practical enough to adapt to do other things later.

BASIC version sanity check
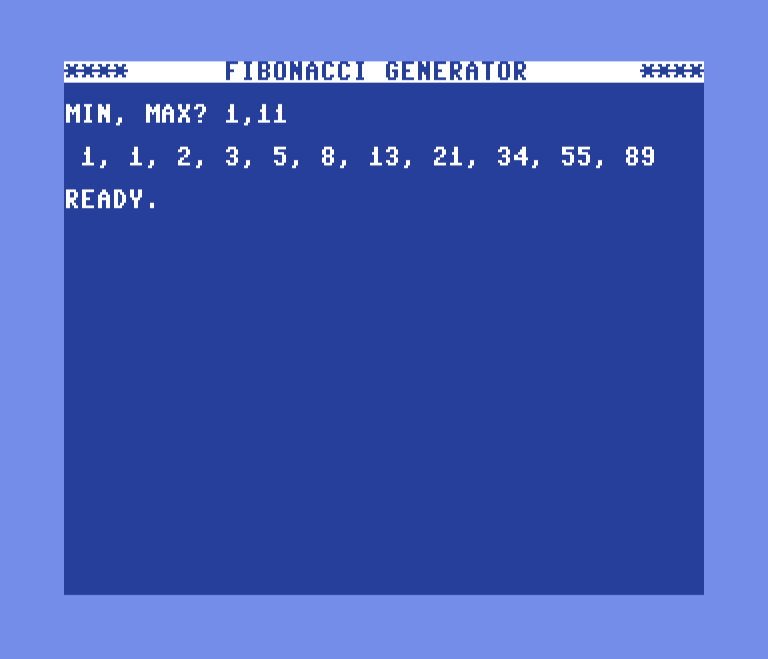
Simple first attempt
We should first see if we can get the values computed into a memory location somewhere. This should be pretty easy. We’ll need two temporary locations to hold the numbers in the sequence we’re working on and a third to be able to swap them in place (gotta save one of them somewhere)
I did this on paper with a pencil.
From “Microcomputer systems principles featuring the 6502/KIM” Camp, Smay and Triska Many books, including “The First Book of KIM” include lookup charts for opcodes. I think it’s good practice to go back to doing this by hand from time to time.
But to save you some heartache in reading my handwriting:
0200 F8 SED
2001 A9 00 LDA #00
2003 85 FA STA FA
2005 85 FB STA FB
2007 85 03 STA 03
2009 A9 01 LDA #01
200B 85 02 STA 02
200D A2 00 LDX #00
200F A5 02 LDA 02
0211 95 05 STA 05,X
2014 85 04 STA 04
2016 65 03 ADC 03
2018 85 02 STA 02
201A A5 04 LDA 04
201C 85 03 STA 03
201E E8 INX
201F E0 0B CPX #0B
0221 30 EC BMI 020F
0223 00 00 BRK
; using temporary storage in $02, $03, $04
; start saving results in $05
I keyed these in by hand, but feel free to enter them however you want. TTY memory entry, or even an assembler. Totally up to you.
Sidebar: if you’ve not hand coded machine language in a while
We’re all used to assemblers doing the heavy calculations. Remember back from Machine Language on the 6502 101 that branch instructions use relative locations. So in our BMI here, we need to jump backward from $0222 to 020F.
Take your destination, subtract the source and add $FF.
$020F - $0222 = -$13
-$13 + $FF = $EC
Our results:
Results $05-$0F Okay, good, that’s what we expected. I stopped at 89 because using BCD mode means we’ll overflow into the next byte to display it. We’ll do that next time.
Displaying the results
There is a straightforward way in the “The First Book of KIM” to display bytes on the seven segments. The rightmost set is at $F9, the middle is $FA and the leftmost is $FB
Simply loading these bytes and calling JSR $1F1F will flash this value on the screen. The book suggests jumping or looping back to it repeatedly so you can see it. We’ll implement a delay here of 255 loops ( $FF ) and then go to the next one.
There is one caveat here. For some reason, jumping to the subroutine at $1F1F clears out the processor registers! This is inconvenient if we’re looping ;-)
(Yes, there are “better” methods for display, we’ll discuss several of them in future articles)
So we’ll need to store those X and Y registers in a temporary location and do what feels like a needless “store and retrieve” on these. There are many ways to accomplish this, and this is just one way. Memory locations $00 and $01 happen to be available for this.
So we loop through the results (counting up) and display them one at a time for a second or two before going to the next one.
0200 F8 SED
0201 A9 00 LDA #00
0203 85 FA STA FA
0205 85 FB STA FB
0207 85 03 STA 03
0209 A9 01 LDA #01
020B 85 02 STA 02
020D A2 00 LDX #00
020F A5 02 LDA 02
0211 95 05 STA 05,X
0213 85 04 STA 04
0215 65 03 ADC 03
0217 85 02 STA 02
0219 A5 04 LDA 04
021B 85 03 STA 03
021D E8 INX
021E E0 0B CPX #0B
0220 30 ED BMI 020F
0222 A0 FF LDY #FF
0224 84 01 STY 01
0226 A2 00 LDX #00
0228 86 00 STX 00
022A B5 05 LDA 05,X
022C 85 F9 STA F9
022E 20 1F 1F JSR 1F1F
0231 A4 01 LDY 01
0233 88 DEY
0234 84 01 STY 01
0236 D0 F6 BNE 022E
0238 A6 00 LDX 00
023A E8 INX
023B 86 00 STX 00
023D E0 0B CPX #0B
023F 90 E9 BCC 022A
0241 00 BRK
0242 00 BRK
0243 00 BRK
; using temporary storage in $02, $03, $04
; start saving results in $05
Simple and easy to understand, if slightly inefficient
Papertape format?
If you have a terminal connection to your KIM-1, loading a papertape format stream will save you some typing:
;180200F8A90085FA85FB8503A9018502A200A5029505850465038509CC
;18021802A5048503E8E00B30EDA0FF8401A2008600B50585F9201F0A18
;1402301FA401888401D0F6A600E88600E00B90E90000000855
;0000030003
How’d we do?
Looks pretty good.
I’ve become a big fan of using the KIM-1 to revisit problems very close to the hardware. It’s not only a good learning platform but seems to help me connect to the historical impact it had, something that a “new retro machine with extended features” somehow lacks.