Permutations of 1 to 9 in Python, BASIC, and 6502 Assembly
By Michael Doornbos
- 6 minutes read - 1082 wordsSomeone asked me this week if I would help him with a graph theory problem on 8-Bit machines. The first task was to get all permutations of 1 to 9. Since the total permutations is 9! (362,880) I knew this would take a while.
Learning without learning, the standard library problem
There are no shortcuts to pretty much anything worth doing. If you fail to learn the basics, then when you get to more advanced things, the basics will feel like black magic, and the thing you’re working on will only make sense on the surface.
Nothing highlights this more than learning basic math and computer concepts like permutations with a built-in library:
from itertools import permutations
# Get all permutations of [1, 2, 3]
perm = permutations([1, 2, 3])
# Print the obtained permutations
for i in list(perm):
print (i)
(1, 2, 3)
(1, 3, 2)
(2, 1, 3)
(2, 3, 1)
(3, 1, 2)
(3, 2, 1)
Well, that was easy! Except we have no idea how the person who programmed the library actually accomplished this.
What actually had to happen to get this list?
If you don’t care, then there are plenty of sites that will just give you the answer and shortcuts. I won’t even be offended if you skip this one.
And do I use this in my everyday solutions or do I roll my own? You bet I use every batteries included feature that the Python standard library provides. And in my career, I’ve certainly skipped learning in favor of expediency. And I’ve regretted that every single time.
Better would at least be something like:
import time
COUNT=0
def swap(A, i, j):
c = A[i]
A[i] = A[j]
A[j] = c
def reverse(A, i, j):
while i < j:
swap(A, i, j)
i = i + 1
j = j - 1
def permutations(s):
global COUNT
if not s:
return []
if len(s) == 1:
return [s]
n = len(s)
chars = sorted(list(s))
while True:
#print(''.join(chars), end=' ') #optionally print them
i = n - 1
while chars[i - 1] >= chars[i]:
i = i - 1
if i == 0:
return
j = n - 1
while j > i and chars[j] <= chars[i - 1]:
j = j - 1
swap(chars, i - 1, j)
reverse(chars, i, n - 1)
COUNT+=1
#print(i)
def runPerms(s):
startTime = time.time()
permutations(s)
print()
print('Count for', s , 'is:' ,COUNT+1)
executionTime = (time.time() - startTime)
print('Execution time in seconds: ' + str(executionTime)[:7])
if __name__ == '__main__':
print("Permutations in Python")
print("MacBook Pro 2Ghz i5 16GB RAM")
print("--------------------------------------")
runPerms('123456')
runPerms('1234567')
runPerms('12345678')
runPerms('123456789')
runPerms('123456789a')
runPerms('123456789ab')
runPerms('123456789abc')
runPerms('123456789abcd')
This is an iterative approach that’s easy enough to follow. Many code examples do this recursively which I don’t think is nearly as easy to follow when learning concepts.
Just for fun:
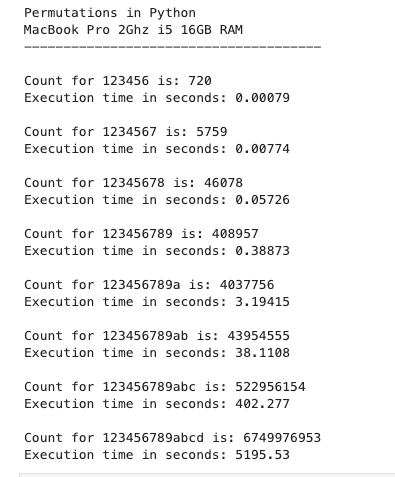
That escalated quickly ;-)
Now let’s do it in BASIC
This is more or less the same algorithm in BASIC. To my eyes, it’s just as easy to follow as the Python version.
5 REM ASSUMES NATURALLY ORDERED ARRAY
10 TI$="000000":CT=0:N=6
100 DIMA(N):FOR I=0 TO N-1:A(I)=I+1 :NEXT
120 GOSUB 400
130 GOTO 120
140 PRINT:PRINT"GOT"CT"IN"TI/60"SECONDS"
199 END
200 ::REM SWAP A I AND J::
210 C=A(I)
220 A(I)=A(J)
230 A(J)=C
299 RETURN
300 ::REM REVERSE A I J::
310 ::REM WHILE I<J::
320 IF I>J THEN 399
330 GOSUB 200
340 I=I+1
350 J=J-1
360 GOTO 320
399 RETURN
400 ::REM PERMUTATIONS OF S
410 GOSUB 900:REM PRINT CURRENT
430 I=N-1
440 IFA(I-1)<A(I)THEN 460
450 I=I-1: IFI=0 THEN 199
455 GOTO 440
460 J=N-1
470 IFJ>I AND A(J)<=A(I-1) THEN J=J-1:GOTO470
480 I=I-1:REM SWAP(A,I-1,J)
490 GOSUB 200
492 I=I+1
495 J=N-1
497 N=N-1
500 GOSUB 300
510 N=N+1
599 RETURN
900 ::REM PRINT DIM::
910 FOR I=0 TO N-1:PRIN TMID$(STR$(A(I)),2);:NEXT:PRINT" ";
920 CT=CT+1
999 RETURN
123456 is pretty quick. It’s faster if we don’t print them, but where’s the fun in that?
For 123456789 it’s 9 factorial. We’ll need to bring out the fastest Commodore: The PAL VIC-20 which completes this in…

Yikes. Almost 30 hours.
6502 Assembly
FYI: I use 6502 as the generic term for all 6502 variants and derivatives.
I happen to have some code for my Enigma machine on Commodore project that I’ve been noodling with for about 6 months where I get all of the possible rotor combinations before we get all of the rotor position combinations.
This code is pretty reusable, so I figured it’s worth sharing. If you see places for improvement, feel free to email me. mike @ this domain works.
Rather than print them, this would be MUCH faster if you just need them in in HEX saved to a memory location. An REU or GeoRAM maybe would be good for this. We’ll do a follow-up article on saving these to an REU and maybe even to disk.
My assembly style
I use Turbo Macro Pro almost exclusively. It has a simple syntax that’s generally very easy to move to other assemblers from. I also don’t care for cross assembling from a modern computer to a vintage computer. It’s just a preference. If I was going to recommend a “modern” assembler, I’d pick KickAssembler.
I don’t usually make shortcuts for locations I happen to have memorized. This is maybe not a great habit, so if you wanted to do something like:
plot = $fff0
chrout = $ffd2
decout = $ab1e
I couldn’t argue with that at all. Self-documenting code is probably a habit I should work on more.
Here’s the code
Nothing new really and the same reverse and swap concept as our Python and BASIC, although this does the permutations left to right instead because it’s how I wanted the enigma rotors to “rotate”.
;---------------------------------------
size = 9
zp1 = $fb
stack .byte 0,0,0,0,0,0,0,0,0,0
numb .byte 9,8,7,6,5,4,3,2,1,0
perms
.block
lda #$00
ldx #size-1
clear sta stack,x
dex
bpl clear
bmi begin
loop lda stack,x
stx zp1
cmp zp1
bcs skip
inc stack,x
tay
txa
lsr a
bcs odd
ldy #$00
odd jsr swap
begin jsr dop
ldx #$01
bne loop ;y not jmp loop
skip lda #$00
sta stack,x
inx
cpx #size
bcc loop
rts
.bend
swap
.block
lda numb,x
pha
lda numb,y
sta numb,x
pla
sta numb,y
rts
.bend
dop
.block
ldx #$00
loop lda numb,x
jsr printbyten
inx
cpx #size
bcc loop
lda #13
jsr $ffd2
rts
.bend
Happy mathing!
I love doing this stuff and would love to hear what you’re doing in computer science. Both ancient machines and modern ones.