Making and Breaking Ciphers with Commodore 64 - The Vigenère Cipher
By Michael Doornbos
- 7 minutes read - 1376 wordsIt is time we start easing into how to break/crack these ciphers. It makes sense then to study the venerable Vigenère cipher. A polyalphabetic cipher that builds on the Caesar cipher. In fact, it’s the same concept except that you rotate the key for every letter. It’s simple to implement and is a lot more secure than a Ceasar Cipher.
The cipher requires we visualize a table that corresponds to each of the 26 possible Caesar Ciphers. Each row is shifted left one place.
We’ll use a repeating keyword that we’ll call the key to use a different alphabet line for each letter of the text we want to encrypt.
Making the table
There isn’t a Commodore 8 Bit machine that can fit this on the screen all at once but it’s easy to implement and looks neat.
Encrypt
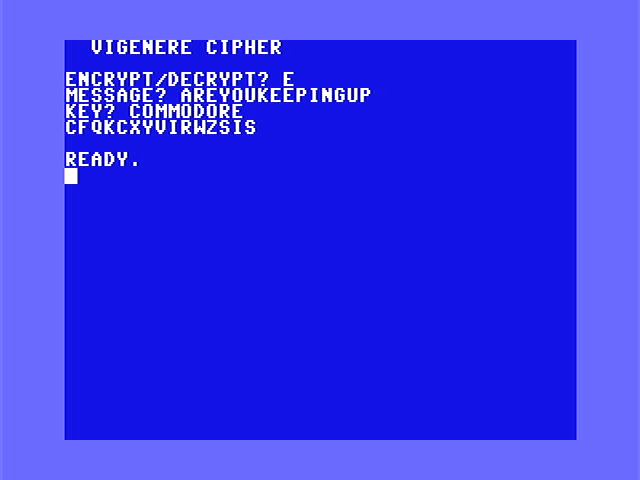
Let’s say we want to send the phrase HELLO with the key CAT.
The first letter of the plaintext, H is paired with C, the first letter of the key.
So use row H and column C of the Vigenère square. The first letter of our encrypted text is then J.
On the second letter of the plaintext, the second letter of the key is used, the letter at row E and column A is E.
Repeat this again for L. Since CAT is shorter than HELLO, when we get to the second L, repeat CAT from the beginning.

So HELLO with the key of CAT encrypts to JEENO
Easy right?
Decrypt
Decryption is backward. Find the row in the table corresponding to the key. Find the position of the encrypted letter in that row, and use the column’s label as the plaintext.
Got it? Good.
Boil it down for a computer program
There are quite a few ways we could implement this. We could create a 26x26 matrix and just do the same thing we do by hand. It would actually be a 27x27 matrix in this case because we’d need a top row set of labels and a left column of labels.
BUT…
If we think of these letters as numbers, which we’d have to do for the indexes of the matrix anyway, it’s pretty easy to shift these on the fly with some simple math. Let’s use A-Z index 0, so 0-25.
Encryption
The plaintext(P) and key(K) are added modulo 26
Ei = (Pi + Ki) mod 26
Decryption key(k) is subtracted from encrypted(E), adding 26 and modulo 26
Di = (Ei - Ki + 26) mod 26
This makes a lot of sense. It will take up little memory and is what we’d have to do to iterate the matrix anyway.
In BASIC
This is should work in most vintage BASIC machines with very little tweaking. It will work in all of the Commodore 8 Bit machines with no changes at all.
1 PRINT CHR$(147);:PRINT" VIGENERE CIPHER"
5 REM VIGENERE CIPHER
10 GOSUB 300:PRINT
20 INPUT"ENCRYPT/DECRYPT";F$
25 IF F$="E" GOTO 40
30 IF F$="D" GOTO 60
40 INPUT"MESSAGE";MS$
45 INPUT"KEY";KS$
50 GOSUB 100:PRINTES$:END
60 INPUT"ENCRYPTED TEXT";ES$
65 INPUT"KEY";KS$
70 GOSUB 200:PRINTMS$:END
99 END
100 REM ENCRYPT
110 L=LEN(MS$):FOR I=0TOL-1
120 J=I-INT(I/LEN(KS$))*LEN(KS$)
130 K=ASC(MID$(KS$,J+1,1))
140 P=ASC(MID$(MS$,I+1,1))
150 E=(P+K):E=E-INT(E/26)*26
160 ES$=ES$+CHR$(E+65)
170 NEXT
199 RETURN
200 REM DECRYPT
210 L=LEN(ES$):FOR I=0TOL-1
220 J=I-INT(I/LEN(KS$))*LEN(KS$)
230 K=ASC(MID$(KS$,J+1,1))
240 E=ASC(MID$(ES$,I+1,1))
250 D=(E-K+26):D=D-INT(D/26)*26
260 MS$=MS$+CHR$(D+65)
270 NEXT
299 RETURN
300 REM MAKE A$
310 A$="":FOR L=0TO25
320 A$=A$+CHR$(65+L)
330 NEXT
399 RETURN
There’s nothing tricky here. We have to use the clumsy MID$ in Commodore BASIC, but it works and is easy to understand once you use it for a while. You’ll notice we’re not using a BASIC extension this time, but instead using our algebra method.
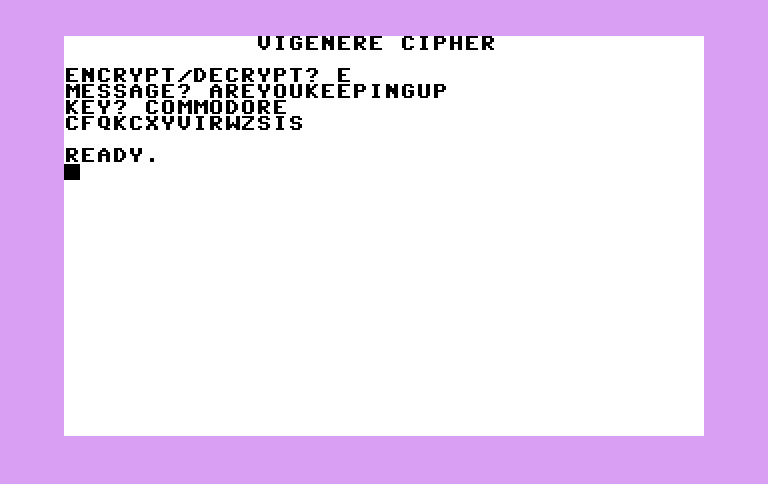
Encrypt on the Commodore Plus/4
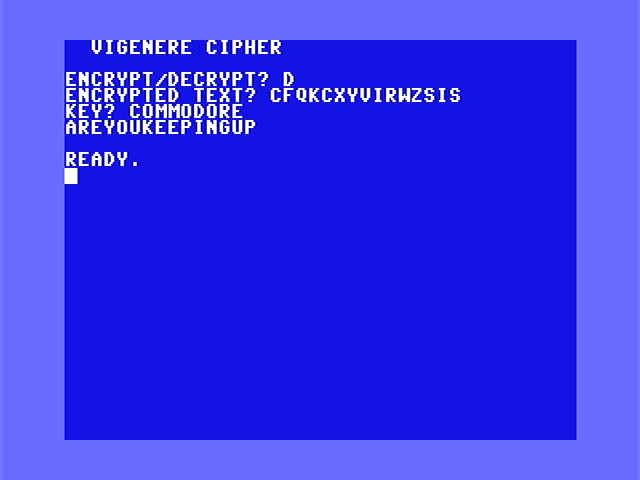
Decrypt on the Commodore 64
Assembly version
We’ll keep the Assembly version as close to the BASIC version above so it’s easy to follow. As we’ve talked about many times now in this series we’re shooting for understanding over efficiency. Feel free to optimize this to your heart’s content. Double dog dare you.
Borrowing that same 24-bit divider we’ve been using. It’s also pretty straightforward.
doencrypt
.block
ldx #0
getlen lda message,x
beq donem
inx
jmp getlen
donem stx messlen
ldx #0
getlenk lda key,x
beq donek
inx
jmp getlenk
donek stx keylen
;loop through message
ldx #0
stx zp3
loop lda message,x
beq done
;get j
jsr cleardivide
ldx zp3
stx dividend
lda keylen
sta divisor
jsr divide24
ldx remainder
;get k
lda key,x ;k in y
sta zp2
;get p
jsr cleardivide
ldx zp3
lda message,x
clc
adc zp2
sta dividend
lda #26
sta divisor
jsr divide24
lda remainder
clc
adc #65
ldx zp3
sta encrypted,x
inx
stx zp3
jmp loop
done
rts
.bend
dodecrypt
.block
ldx #0
getlene lda encrypted,x
beq donee
inx
jmp getlene
donee stx enclen
ldx #0
getlenk lda key,x
beq donek
inx
jmp getlenk
donek stx keylen
;loop through message
ldx #0
stx zp3
loop lda encrypted,x
beq done
;get j
jsr cleardivide
ldx zp3
stx dividend
lda keylen
sta divisor
jsr divide24
ldx remainder
;get k
lda key,x ;k in y
sta zp2
;get p
jsr cleardivide
ldx zp3
lda encrypted,x
sec
sbc zp2
clc
adc #26
sta dividend
lda #26
sta divisor
jsr divide24
lda remainder
clc
adc #65
ldx zp3
sta message,x
inx
stx zp3
jmp loop
done
rts
.bend
I’ve added the jsr cleardivide which just ensures that the memory locations are clear before we do any division. In practice, this wasn’t needed since we’re nowhere near overflowing a single byte register, but it’s a good idea to think about this.
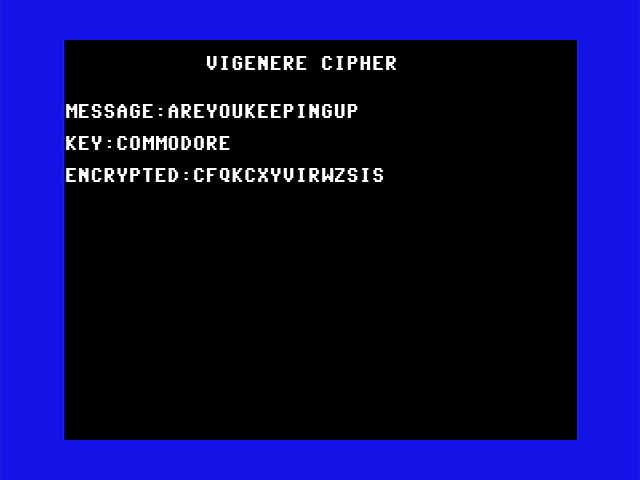
Assembly version on a Commodore 128
As you might expect, the version is dramatically faster.
Breaking it
If you’ve not stumbled on Nils Kopal’s excellent and free Cryptool project I suggest you check it out. We’ll use it, and a modern computer (MacBook Pro 2020 version) to try and break this cipher. A couple million calculations per second make quick work of this one.
Let’s work on this message.
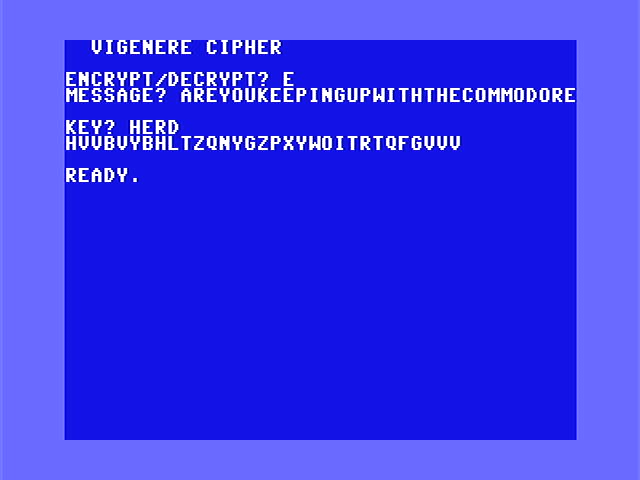
Most “classical” ciphers are susceptible to word frequency analysis and index of coincidence. These attacks do require a longer message and work better on a shorter key. The shorter the message and the longer the key, the harder it is to do this.
The default analyzer for Cryptool does this analysis using the well-known hill-climbing method. It makes an initial guess and if it’s better than the one before it iterates on this new result. This program on a MacBook with a quad-core Intel i5 and 16GB of RAM cracks this in 2 seconds.
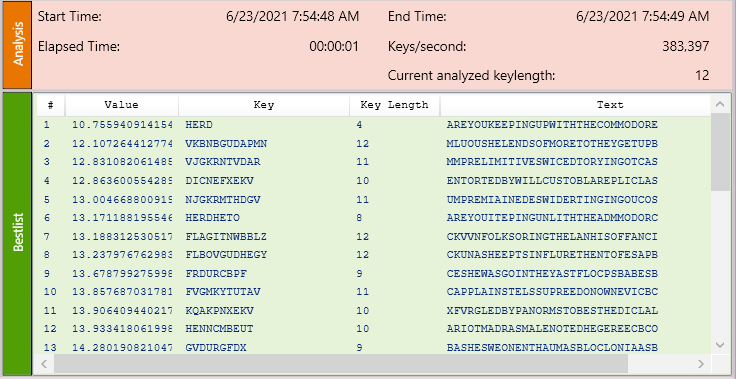
Screenshot from Cryptool2 (cryptool.org)
If we use a shorter message and longer key, the method has a harder time making sense of it. There isn’t enough repeatable data and it looks too much like noise to the algorithms.
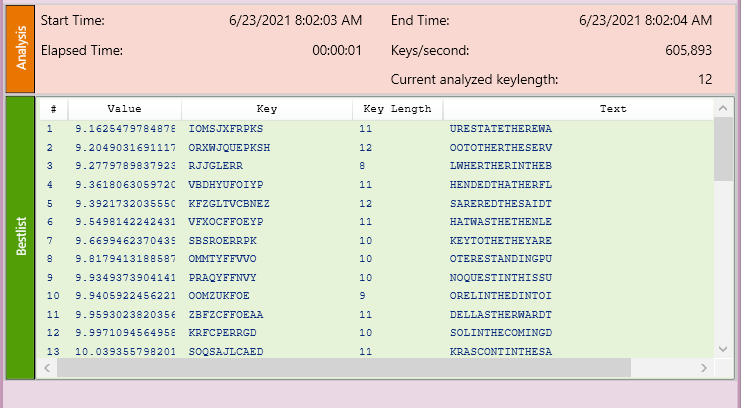
It doesn’t get it at all, but there are some interesting combinations that created English words. This highlights how finicky some of these attacks can be.
Remember: short messages with longer nonsensical keys are your friend to fool your attacker.
What about cracking it on the Commodore?
We will be doing these methods on the Commodore later in the series. We’ve still got several interesting ciphers to implement before we start doing more advanced code that cracking these will require.
Extra credit
I enjoy using these classical ciphers a lot. This one requires nothing but the table and a pencil, so it’s a fun one to introduce people to the world of cryptography.
Some fun things to try:
- Try the BASIC code out on different computers of the era. If you’re lucky enough to have old computers, give this a try. There are many EXCELLENT emulators for almost any computer you can think of as well. Or try a modern computer. BBCBasic is available for your modern computer and this will work with some small changes. I’m going to try it on my Sharp PC-4 pocket computer from the 80s.
- Optimize that Assembly code as much as possible. The faster we can get it to run, the faster our cracking routines will run later on when we start doing those.
- Try out Cryptool for yourself. It’s a wonderful tool. Nils also has a retro youtube channel worth checking out.
Don’t forget to have fun!