We’re on ANOTHER random number generation technique today. Let’s work on the Lagged Fibonacci Sequence, a fun way to use the Fibonacci Sequence on itself to generate pseudo-random numbers.

One of our long term goals is to add a bunch of tools to our toolbox. Making reusable components makes doing more complicated things easier. You can rifle through your toolbox in hopes of an “Oh, I already have something we can use for this part!”.

What’s the Fibonacci sequence again?

It’s a simple pattern that appears in a kinds of places in nature. For example, tree branches follow a Fibonacci pattern. Who knew trees were good at math?

In a series, the next value is the sum of the previous two.

So if we start with 0 and 1, next is… 1. Then…

0,1,1,2,3,5,8,13,21,34...

Let’s do this on a VIC-20

The lowly VIC 20 doesn’t get much love since it’s often overshadowed by the Commodore 64. What most people don’t know is that for raw calculations, it’s actually faster than a 64. Yes there are benchmarks later, calm down.

We need to get two values and add them to get a third. Lets try to use GOSUBs to organize our code so we can add stuff to our toolbox. You never know when you might need a Fibonacci series generator in BASIC. Could happen.

10 F=0:FOR C=0 TO 20
20 GOSUB 100
30 PRINT F;
40 NEXT
50 END
100 REM *** FIBONOCCI ***
110 IF C = 0 THEN F=0:RETURN
120 F1=0:F2=1
130 FOR I=2 TO C
140 F=F1+F2:F1=F2:F2=F
150 NEXT
160 RETURN

Lagged Fibonacci

Used most famously in FreeCiv, but even Oracle databases use it in some places, the Lagged Fibonacci Generator is another way to generate pseudo random numbers with okayish randomness properties.

Directly from Wikipedia:

For the generator to achieve this maximum period, the polynomial:

y = xk + xj + 1 must be primitive over the integers mod 2. Values of j and k satisfying this constraint have been published in the literature.

Clear as mud? It’ll be easier to visualize in the code.

We’re going to use k=3 j=7 for this example to keep this short. Feel free to use our example here and expand it to various keys and test your result.

10 DIM S(8):S$="8675309":F=0:MAX=255:J=3:K=7
15 FOR I=1 TO 7:S(I)=VAL(MID$(S$,I,1)):NEXT I
19 FOR C=1 TO 10
20 GOSUB 110
30 NEXT C
90 END
100 REM *** LAGGED FIB ***
110 F=S(J)+S(K):IF F>255 THEN F=F-MAX+1
115 PRINT F;
120 FOR I=1 TO 6:S(I)=S(I+1):NEXT I:S(7)=F
130 RETURN

If we run this 10 times we get some random numbers:

Monte Carlo Method to test randomness

We’ll do a bunch of iterations over this subroutine in a second. First we should talk about how random this may or may not be.

As you might expect, there are many ways to test if a series is random. The Monte Carlo of Pi method is an excellent way to inefficiently estimate Pi, but another use is to test for randomness. The closer your results are to pi, the more random your series is.

We will take our random numbers and scale them between 0.0 and 1.0, then using two values at a time and calculate ​the square root of _x_2+_y_2 . If this value is less than or equal to 1, we place in the circle (with a radius of 1), otherwise it is outside the circle. The estimation of PI is then four times the number of points in the circle (M) divided by the total number of points (N).

We’ll add it as a GOSUB starting at line 300. Lines 345-390 do a little printing and formatting to help see what’s happening.

1 C=100
5 TI$="000000" 
10 J=3:K=7:DIMS(8):S$="8675309":F=0:MAX=255:IN=0:OUT=0
15 FORI=1TO7:S(I)=VAL(MID$(S$,I,1)):NEXT
20 DIMV(C):FOR N=0TOE
30 GOSUB 100
50 V(N)=F:PRINTV(N);
60 NEXT
65 GOSUB 300
70 PRINT:PRINT"JIFFIES:"TI
80 END
100 REM *** LAGGED FIB ***
110 F=S(J)+S(K):IFF>255THENF=F-MAX+1
120 FORI=1TO6:S(I)=S(I+1):NEXT:S(7)=F
130 RETURN
200 PRINT"->";:FORP=1TO7:PRINTS(P);:NEXT:PRINT: RETURN
300 REM *** Monte Carlo *** 
305 PRINT:FORN=0TOC-1 STEP2
310 X=(V(N)-MAX/2)/(MAX/2)
320 Y=(V(N+1)-MAX/2)/(MAX/2)
330 Z=SQR(X^2+Y^2)
340 X$=STR$(X):Y$=STR$(Y):Z$=STR$(Z)
345 PRINTLEFT$(X$,4);:PRINTLEFT$(Y$,4);:PRINTLEFT$(Z$,4)
350 IF Z<1 THENIN=IN+1
360 IF Z>1 THENOUT=OUT+1
365 NEXT
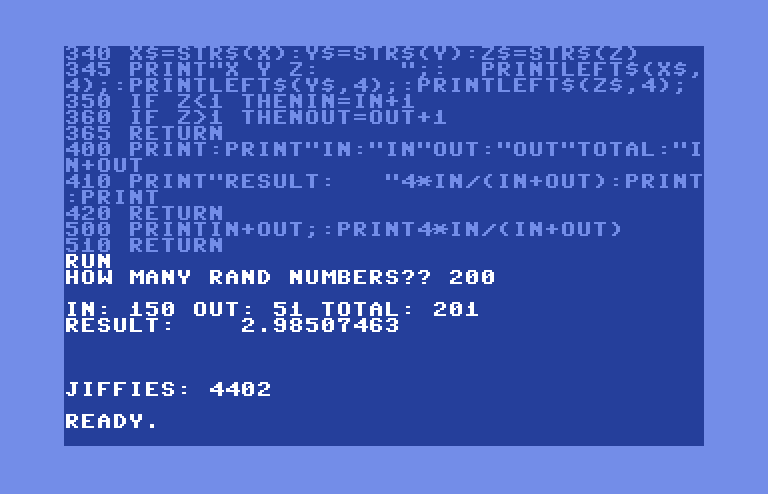
370 PRINT:PRINT"IN:"IN"OUT:"OUT
380 PRINT:PRINT"RESULT:"4*IN/(IN+OUT)
390 RETURN

Embracing the constraints

We’re doing this on an unexpanded VIC-20 on purpose. Partly because it’s cool and partly because it almost immediately shows us a problem with our implementation above. Constraints can be a good thing.

This implementation so far reflects my modern approach to solving this problem where memory is cheap and plentiful.

My daily driver computer is a Mac with 3.2x1010 Bytes of RAM (32GB).

The VIC 20 has 3583 Bytes. Slightly less.

On my Mac, I don’t think much of making an array of 50k values. On a VIC-20, even a 100 value array is pretty large. Remember, we have 3583 Bytes to work with. A DIM(100) takes up something like 500 Bytes on a Commodore plus the values in the DIM.

So what do we do about this if we want to calculate this to 50k pairs?

We have limited RAM, but “unlimited” CPU time if we’re willing to wait on a 1 Mhz CPU. So let’s rethink this:

1 C=100
5 TI$="000000" 
10 J=3:K=7:DIMS(8):S$="8675309":F=0:MAX=255:IN=0:OUT=0
15 FORI=1TO7:S(I)=VAL(MID$(S$,I,1)):NEXT
20 FOR N=0TOC
30 GOSUB 100
40 FX=F:PRINT"NEXT PAIR:";:PRINTFX;
45 GOSUB 100
50 FY=F:PRINTFY;
60 GOSUB 300
65 GOSUB400
70 NEXT
75 PRINT:PRINT"JIFFIES:"TI
80 END
100 REM *** LAGGED FIB ***
110 F=S(J)+S(K):IFF>255THENF=F-MAX+1
120 FORI=1TO6:S(I)=S(I+1):NEXT:S(7)=F
130 RETURN
200 PRINT"->";:FORP=1TO7:PRINTS(P);:NEXT:PRINT: RETURN
300 REM *** MONTE CARLO ***
305 PRINT
310 X=(FX-MAX/2)/(MAX/2)
320 Y=(FY-MAX/2)/(MAX/2)
330 Z=SQR(X^2+Y^2)
340 X$=STR$(X):Y$=STR$(Y):Z$=STR$(Z)
345 PRINT"X Y Z:";:PRINTLEFT$(X$,4);:PRINTLEFT$(Y$,4);:PRINTLEFT$(Z$,4);
350 IF Z<1 THENIN=IN+1
360 IF Z>1 THENOUT=OUT+1
365 RETURN
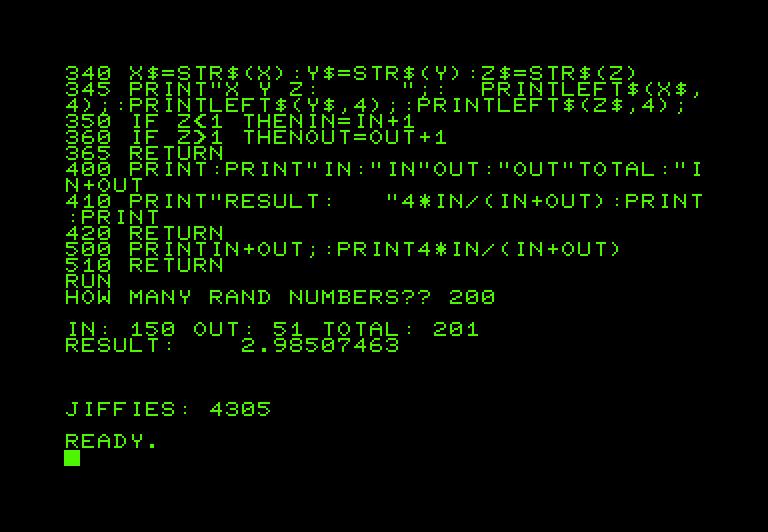
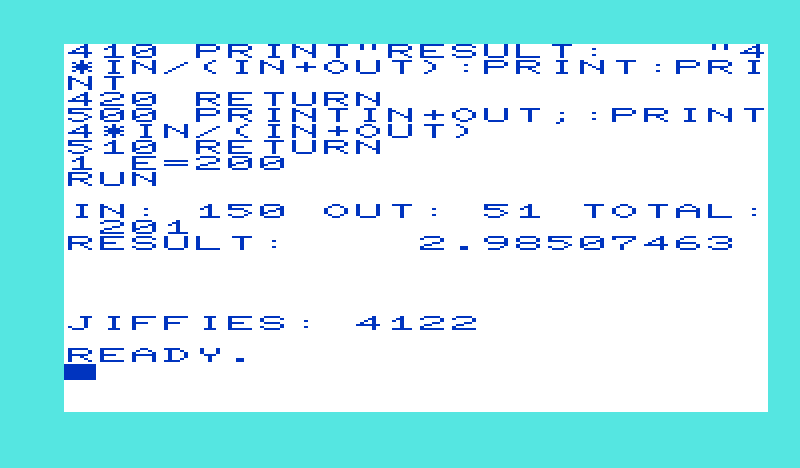
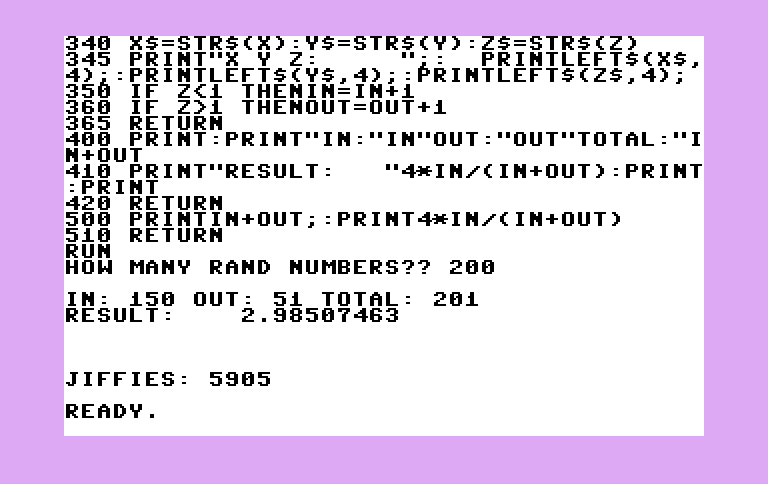
400 PRINT:PRINT"IN:"IN"OUT:"OUT"TOTAL:"IN+OUT
410 PRINT"RESULT:"4*IN/(IN+OUT):PRINT:PRINT
420 RETURN

Much better. Now we’re limited by the CPU speed and wont run out of RAM.

Benchmarking

We can’t do these without benchmarking on different systems can we?

Too fun.

Lets skip the printing along the way and just loop through a bunch of them:

Monte Carlo Visual

It’s fun to visualize the dots inside and outside the circle. If we expand our constraints just a little and add the Super Expander Cartridge to our VIC 20, doing a visual is pretty easy.

Assembly version

I don’t want to be called lazy, especially on the internet where words mean the difference between life and death.

Or is it “the angry internet people don’t matter”. Anyway, it’s one of those…

If we want to do any large calculations of this or use it in a game we need to implement it in Assembly anyway.

Assembly Fibonacci

Let’s make a routine that’s as close to the BASIC version as we can. It’s some simple 16 bit addition which we’ve done before:

fib
         ldx #0
         lda #0
         jsr $ddcd
         lda #32
         jsr $ffd2

         ldx f2    
         lda f2+1
         jsr $ddcd
         lda #32
         jsr $ffd2
     
loop     clc
         lda f1
         adc f2
         sta f0
         lda f1+1
         adc f2+1
         sta f0+1

         lda f2
         sta f1
         lda f2+1
         sta f1+1

         lda f0
         sta f2
         lda f0+1
         sta f2+1

print    ldx f0
         lda f0+1
         jsr $ddcd
         lda #32
         jsr $ffd2
         
         inc c
         ldx c
         cpx #23
         bne loop

         rts

f0       .byte 0,0
f1       .byte 0,0
f2       .byte 1,0
c        .byte 0

Lagged Assembly

We’re going for as close to the BASIC implementation as possible here as well. This is about understanding, not breaking speed or efficiency records.

j        .byte 2
k        .byte 6
s        .byte 8,6,7,5,3,0,9
f        .byte 0
fx       .byte 0
fy       .byte 0

max      = 255
slen     = 6  ;zero based
zp1      = $fb
decout   = $ddcd ; change to $bdcd on C64

lagfib
         .block
loop     ldx j
         ldy k
         lda s,x
         clc
         adc s,y
         cmp #max
         bcc ahead
         sec
         sbc #max
ahead
         sta f

         ldx #0
loop2    lda s+1,x
         sta s,x
         inx
         cpx #slen
         bne loop2

         lda f
         ldx #slen
         sta s,x

print   
         ldy #0
         sty zp1
loop3
         lda s,y
         tax
         lda #0
         jsr decout
         lda #$20
         jsr $ffd2
         inc zp1
         ldy zp1
         cpy #slen+1
         bne loop3

         lda #$0d
         jsr $ffd2
done
         rts
         .bend

That’s it. Now we have an okayish Pseudo Random Number generator that 8 Bit Computers can do fairly easily.

Optimize

In your spare time it’s fun took for places to optimize all of these loops both in the BASIC versions and Assembly. Try them out and see how fast you can make it. I want to hear about your improvements to what we’ve done here.

• C64
• Code
• Commodore
• How-To
• Retro
• Security
• VIC-20