Making and breaking Ciphers on the Commodore 64 Part 12 - Pontifex - Solitaire from Cryptonomicon
By Michael Doornbos
- 9 minutes read - 1713 wordsCryptonomicon Pontifex/Solitaire
We’re back to my favorite book for another round. We’ve done quite a bit with Cryptonomicon so far. One of my favorite moments is when Enoch Root introduces a cipher that two prisoners used to communicate using just a humble playing card deck.

Drawing of the mine in the book
Bruce Schneier
Pontifex is an encryption method you can do with another person using a deck of cards. It was invented for “Cryptonomicon” for Neal Stephenson by Bruce Schneier. He called it Solitaire. In the book it’s called Pontifex to obfuscate the method a little bit.
I happen to have met Captain Gerald “Jerry” Coffee in 2000. He and his fellow prisoners invented a communication methodology in a POW camp in Vietnam, so the story is not as crazy as you might think.
What? You haven’t invented your own encryption method to communicate with other field agents? Slacker.
How this works
This algorithm generates key stream values by moving cards within the deck. The stream values depend on the initial order of the deck.
Bruce published a VERY thorough article in 1999 on how this works in a couple thousand words of detail.
The short version is:
We need two jokers and they need to be different somehow. In my deck I’ve got a red and a black. I’m calling the red joker A and the black joker is B simply because it’s easy for me to remember that B is for black.
You’ll need to shuffle the deck and then make the second deck look exactly like the first deck. You get one, your partner gets the other. Now go off and do some secret spy stuff. We’ll wait…
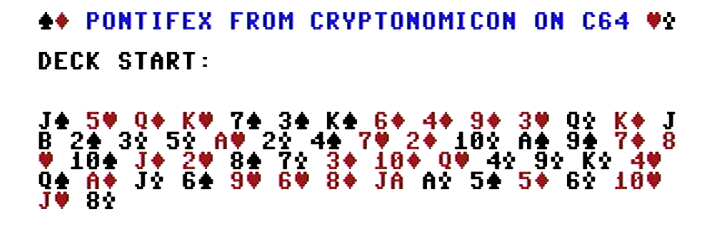
Our deck looks like this to start:
Let’s use our standard “ARE YOU KEEPING UP”. Just to prove the concept, we’ll just use ARE like we’ve done in a few examples before. This takes a… while. We don’t want to be here all week.
We need to change these letters to numbers. We’ll use 1-26 to represent the letters.
A=1 R=18 E=5
1 18 5
Let’s get our keys to encrypt this thing:
Locate the A joker and move it down the deck by one place. If it is the last card, it becomes the second card. Remember to think of the deck as a continuous stream. It wraps around. So now our deck looks like this:
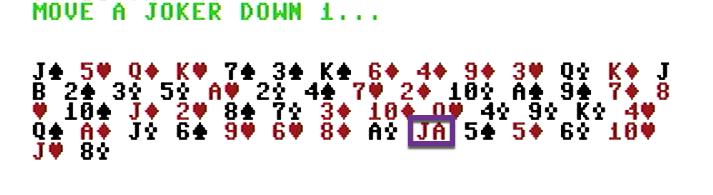
Locate the B joker (value 28) and move it down the deck by two places. The same wrap around rules apply as before. The deck “never ends”.
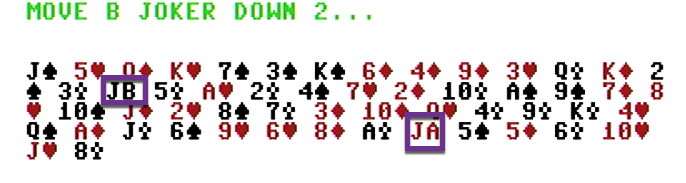
Perform a “triple cut”: split the deck into three sections. Everything above the top joker (may or may not be the A joker, it’s not in our example) and everything below the bottom joker will be swapped. The jokers themselves, and the cards between them stay where they are.
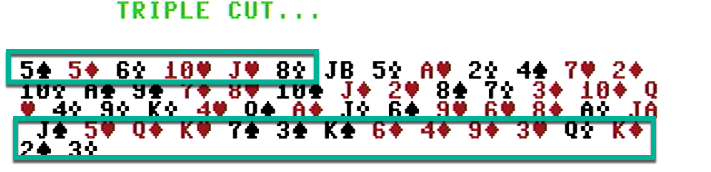
Now we do a “count cut”. The cards are valued 1 to 53 (both jokers are 53). They are “scored” in bridge order, So Ace through King of Spades, Diamonds, Hearts and Clubs. So a King of Hearts is 39
Count down from the top of the deck this many cards and take it and the cards above it and put them just above the last card in the deck.

Now, look at the value of the top card. Again, either joker counts as 53. Count down this many cards (leave it in place, this step does not change the deck). If the card counted down to is a joker, ignore this round and do it again from here.
Whatever the value of the card is you’ve counted down to is your key. Do this two more times to get keys for ARE. You should end up with:
22 26 3
Add the plaintext number stream to the key stream numbers, modulo 26. (All this means is, if the sum is more than 26, subtract 26 from the result.) For example, 1+1=2, 26+1=27, and 27-26=1, so 26+1=1.
Now add 22 to our letter A and the first number of our encrypted message is a 23.
Now convert them back to letters:
1 18 5
+22 26 3
-------------
23 44 8
-26
-------------
23 18 8
W R H
Now we’ll send this WRH to whoever we’re exchanging messages. She will then get the next three keys in the stream (they’ll be identical to yours since your decks start out in exactly the same order) and does this backwards.
Instead of adding the key stream and ciphertext, she’ll subtract the keystream numbers from the ciphertext numbers, modulo 26. For example, 22-1=21, 1-22=5. (If the first number is less than or equal to the second number, add 26 to the first number before subtracting. So 1-22=? becomes 27-22=5).
W R H
23 18 8
- 22 26 3
------------
1 -8 5
+26
------------
1 18 5
A R E
It works. Now we secretly exchanged… ARE.
Exciting.
Problems in implementing
This certainly checks the box of not needing much to implement. It also doesn’t look suspicious if either of you is caught with a shuffled deck of playing cards.
But it’s extremely easy to get your deck out of sync.
I picked up two new card decks for this project. Naturally, they are ACE cards. You know me and airplanes…
Have you ever noticed just how slippery a new deck of cards is? This presents quite a challenge when keeping them in a very precise order is crucial.

The other thing that’s difficult about this method is that there’s no real way to tell if you’ve received all of the messages or if they were received in the correct order. One little screw up and you’re toast.
Code
Why a Commodore version?
Well besides “just because”, this method does work pretty well, but IT. IS. SLOW.
I’ve been doing these for about a week and can now get a key from the stream about every 90 seconds. At this speed I worry about messing up, which as we discussed before makes the deck you have in your hand completely useless.
Let’s do this one entirely in BASIC. Since we’ll have to keep track of several arrays and slice through them, it’ll be hard enough to do with the DIM built in to BASIC 2.0
Key Variables
We’ll need 3 arrays for this:
20 DIMD$(54):DIMTMP(54):DIMV(54)
D$ is the cards themselves that we want to display. This is not strictly necessary since we only care about their values, but it looks cool and we want to look cool right?
I played around with a couple different ways to procedurally generating the deck the way that I wanted, but I eventually ended up hard coding the deck to give me more presentation flexibility:
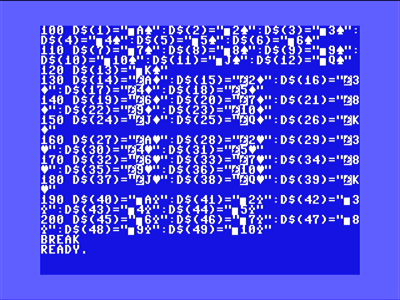
V is where we’ll hold the values of the cards. We’ll use index 1 here not index 0 because then the value of the card will be its position.
We’ll need to have the deck keyed somehow. You can either initially shuffle:
1210 FORJ=1TO53
1220 J%=J+INT(RND(1)*(55-J))
1230 TEMP=V(J):V(J)=V(J%):V(J%)=TEMP
1240 NEXTJ:RETURN
But it makes sense to have a way to set the deck up the way we have it set up with the person we’re exchanging messages with. So lets use DATA statements and just load them:
360 FORN=1TO54:READC:V(N)=C:NEXTN
...
5000 DATA 11,31,25,39,7,3,13,19,17,22,29
5010 DATA 51,26,54,2,42,44,27,41,4,33
5020 DATA 15,49,1,9,20,34,10,24,28,8,46
5030 DATA 16,23,38,43,48,52,30,12,14,50
5040 DATA 6,35,32,21,53,40,5,18,45,36
5050 DATA 37,47,10
TMP is were we are storing the array values when we do the cuts. BASIC 2.0 doesn’t have array slicing or appending so we’ll have to copy our values into TMP and then copy them back to V
Find the Joker A and move it down one in the deck:
1500 REM *** FIND JA
1520 FOR J=1TO54:IFV(J)=53THENJA=J
1530 NEXTJ:PRINT"JA:"JA
1535 PRINT"MOVE A JOKER DOWN 1..."
1540 IFJA<54THENGOTO1560
1550 FORJ=53TO3STEP-1:V(J+1)=V(J):NEXTJ:V(2)=53:RETURN
1560 TEMP=V(JA+1):V(JA+1)=53:V(JA)=TEMP:JA=JA+1
1590 RETURN
Find the Joker B and move it down two in the deck:
1700 REM *** FIND JB
1720 FOR J=1TO54:IFV(J)=54THENJB=J
1730 NEXTJ:PRINT"JB:"JB
1735 PRINT"MOVE B JOKER DOWN 2..."
1740 IFJB<53THENGOTO1780
1750 IFJB=54THENGOTO1760
1755 IFJB=53THENGOTO1770
1760 REM DOWN TWO
1765 FORJ=53TO3STEP-1:V(J+1)=V(J):NEXTJ:V(3)=54:RETURN
1770 FORJ=52TO2STEP-1:V(J+1)=V(J):NEXTJ:V(2)=54:RETURN
1780 T=V(JB+1):TTWO=V(JB+2):V(JB+2)=54:V(JB)=T:V(JB+1)=TTWO:JB=JB+2
1790 RETURN
Now do the triple cut. We need to put the cards into TMP to do this:
1900 REM**TRIPLE CUT
1910 IFJA>JBGOTO1960
1920 FORJ=JA-1TO1STEP-1:TMP(55-JA+J)=V(J):NEXTJ
1925 IF JB=54GOTO1940
1930 FORJ=JB+1TO54:TMP(J-JB)=V(J):NEXTJ
1940 FORJ=JATOJB:TMP(55-JB+J-JA)=V(J):NEXTJ
1959 RETURN
1960 REM DO JA AND JB BACKWARDS
1970 FORJ=JB-1TO1STEP-1:TMP(55-JB+J)=V(J):NEXTJ
1975 IF JA=54GOTO1990
1980 FORJ=JA+1TO54:TMP(J-JA)=V(J):NEXTJ
1990 FORJ=JBTOJA:TMP(55-JA+J-JB)=V(J):NEXTJ
1999 RETURN
Copy TMP to V:
2000 REM *** COPY TMP TO V
2010 FOR J=1TO54:V(J)=TMP(J):NEXTJ:RETURN
Do the count cut:
2100 REM** CUT COUNT CC IS COUNT CARD**
2110 CC=V(54):IF CC=54ORCC=53GOTO2180
2120 FORJ=1TOCC:TMP(53-CC+J)=V(J):NEXTJ:TMP(54)=V(54)
2130 FORJ=CC+1TO53:TMP(J-CC)=V(J):NEXTJ
2190 RETURN
Copy TMP to V again:
2000 REM *** COPY TMP TO V
2010 FOR J=1TO54:V(J)=TMP(J):NEXTJ:RETURN
And finally count down the value of the top card and get the value of the resulting card:
2210 IF V(V(1))>26 THEN PRINT "KEY IS:"V(V(1))-16:RETURN
2220 PRINT "KEY IS:"V(V(1)):RETURN
Running it
If we loop back to the start of the moving jokers subroutine, this can be continued indefinitely to get as many keys out of the stream as you want. Even poorly written in BASIC 2.0 on a 40 year old computer it is many times faster than doing it by hand.
The moral of the story?
Remember to always lug around your Commodore into the field when you want to implement a cipher that can be done with a deck of cards. Very practical.

Other computers of the era
This should work on anything that speaks at least BASIC 2.0 from the 80s with very minor changes. I confirmed it works fine on a VIC-20 and a Commodore 128. Other than the colors of the cards I used, it should work fine on the PET as well. It would be cool to see this on other machines like the Sinclair and Amstrad.
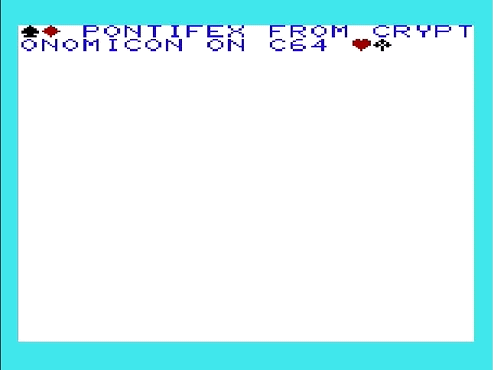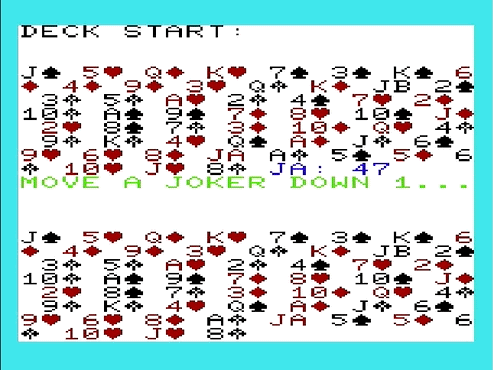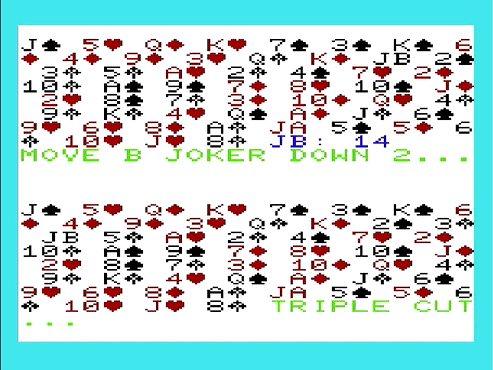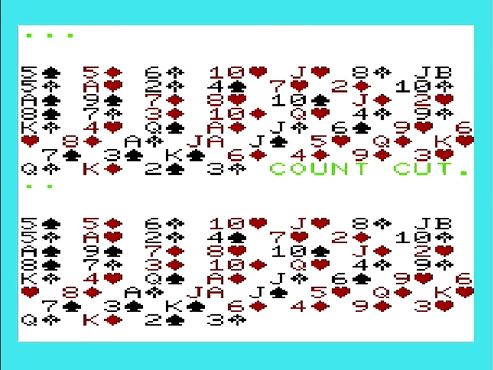
Cryptanalysis
This has been proven to be ineffective against modern attacks. Sorta. Some tips to make it more secure:
- Keep your messages very short. This is a good practice with any encryption you use. It decreases the effectiveness of frequency attacks
- Change the deck key often
Extra Credit
- We’d all like to see this implemented on other vintage machines. Please give this a try
- Can you think of better ways to slice the arrays? I’ll bet you can.