Making and Breaking Ciphers with a Commodore 64 - Part 3: The Caesar Cipher
By Michael Doornbos
- 6 minutes read - 1274 wordsWell here we are at part three and it’s a lot to pack into one page.
Let’s build upon [what I called the Shift Cipher] and implement what is often referred to as the Caesar Cipher, although there is much debate on when this was really first done.
The idea is the same as our Part 2. We’re going to shift the letters a given number of times, but this time we’re going to do the encoding and decoding programmatically instead of just creating a reference to do it by hand.
Reconnaissance
You’re at a big advantage if you can figure out what the cipher is in advance. Maybe you overheard a conversation about what cipher they used, or maybe you were much more invasive about learning it.
In codebreaking, a huge percentage of the work is reconnaissance. The more you can find out about a target message or group you’re targeting, the better chance you have of figuring what they’re using and the kinds of things they might be communicating.
We’ve intercepted a message from a morse code broadcast (just go with it).
NER LBH XRRCVAT HC
The Setup
We know that this is a Caesar cipher because someone had loose lips at social event and now we’re at a big advantage. What’s the advantage? Well this cipher probably only has a handful of possible keys as it’s typically done with letters and sometimes numbers. There are ways to further obfuscate the possible combinations, but in this case our target didn’t do that.
We should be able to get all possible combinations of this message and find the correct one in short order.
Python Caesar encrypt version
Lets implement a Caesar encryption script first to set the groundwork to help us visualize the Assembly version later.
#!/usr/bin/env python
message = 'ARE YOU KEEPING UP'
key = 13
LETTERS = 'ABCDEFGHIJKLMNOPQRSTUVWXYZ'
encrypted = ''
for letter in message:
if ord(letter) == 32: # is this a space?
encrypted = encrypted + ' '
else:
letterIndex = LETTERS.find(letter)
encryptedIndex = letterIndex + key
if encryptedIndex >= len(LETTERS):
encryptedIndex = encryptedIndex - len(LETTERS)
elif encryptedIndex < 0:
encryptedIndex = encryptedIndex + len(LETTERS)
encrypted = encrypted + LETTERS[encryptedIndex]
if __name__ == '__main__':
print(encrypted)
This is pretty straightforward. One thing to note is that I intentionally skip the spaces and leave it in the encrypted message as a space. If you want to include it in the LETTERS string and shift it 13 like the rest of the letters, that’s okay too.
Commodore Version
We’re going to test just the uppercase alphabet like above. Both for simplicity of understanding the implementation and so I can fit all of the guesses on a 40 year old computer screen that only has 40 columns by 25 rows of text ;-)
The letters we have from the ASCII table are:
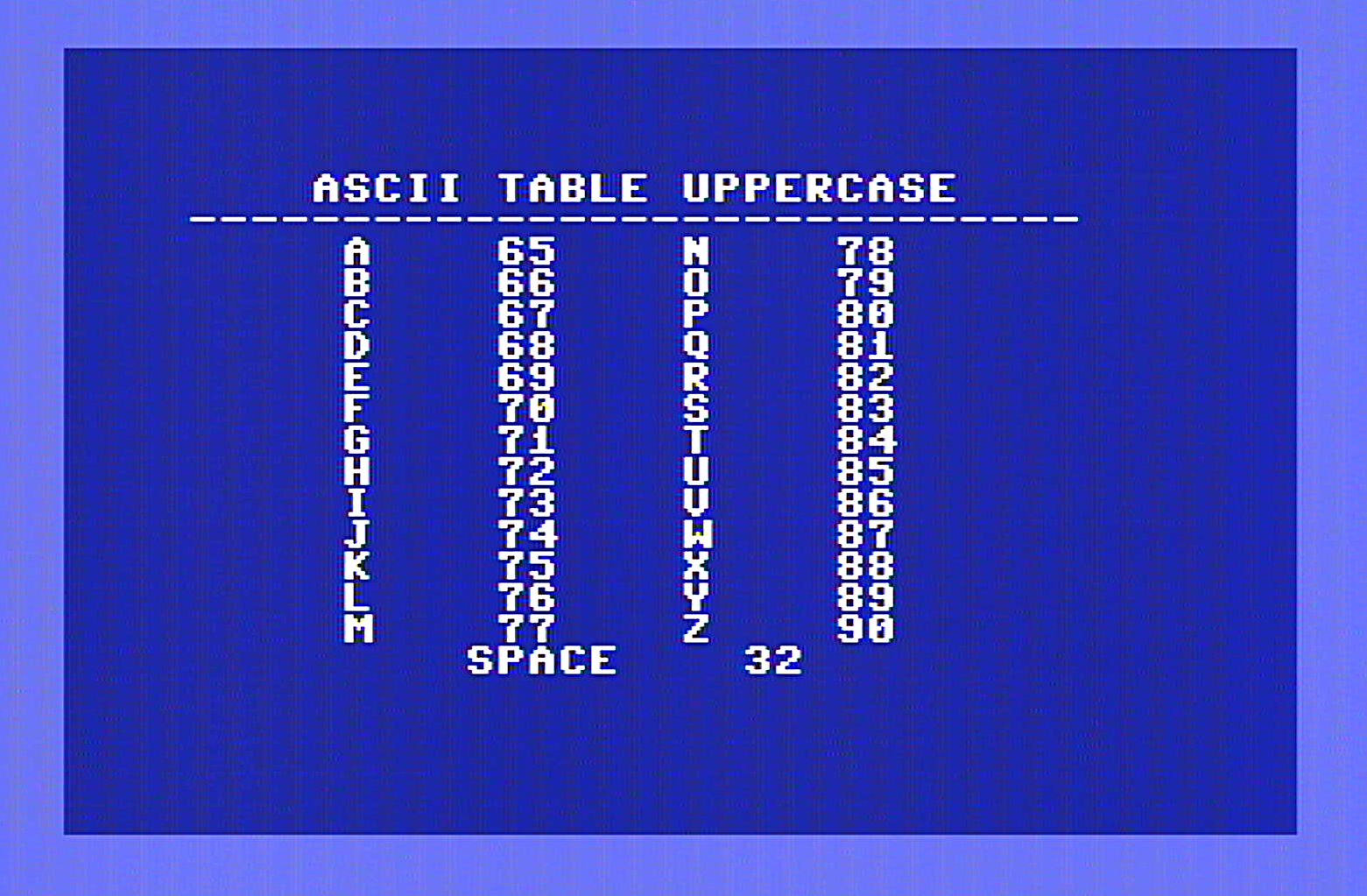
Let’s put these into a table so we can easily iterate over them, shift them and look for matches:
letters .byte 65,66,67,68,69,70 ; A-F
.byte 71,72,73,74,75,76 ; G-L
.byte 77,78,79,80,81,82 ; M-R
.byte 83,84,85,86,87,88 ; S-X
.byte 89,90 ; Y-Z
If we store the message as a null terminated string the Assembler will automatically convert these to the ASCII codes. Just remember that if you’re looking at these in a monitor that they actually get stored as hex values from $41-$5A. They are the same values, I just personally find ASCII values easier to represent in decimal since I’m already familiar with their decimal values. Some people like to do all hex in Assembly. You do you.
String Lengths
We’ll need a routine that checks for the length of something and stores it somewhere for the rest of this Cipher series, so let’s make one now. We’ll use variations of:
messagelength
ldx #0
checkcr cmp message,x
beq done
inx
jmp checkcr
done stx messagelen
rts
Encrypt
Now let’s encrypt our message. We’ll be using the “ARE YOU KEEPING UP” phrase again. Note that my Assembler strings are typed in lowercase, but they are actually Assembled to their uppercase values. Check your Assembler documentation on this.
We’ll again check if it’s a space and jump ahead if it is, followed by getting our index position and then adding 13 in this case. Next we check for if we need to wrap back around because we’ve reached the end of the alphabet and handle that with BCC, or branch if carry clear.
I find it helpful to think of “branch if carry clear”, BCC as less than ("<") and “branch if carry set”, BCS as greater than or equal (">=").
chrout = $ffd2
plot = $fff0
screen = $0400
messtmp = $fb
encryptmp = $fd
messagelen = $fc
key .byte 13 ; $hex $0D
message .null "are you keeping up"
encrypted .null " "
doecrypt
.block
ldy #0
ploop lda message,y
cmp #32
beq space ;skip ahead if it's a space
sta messtmp
ldx #0
loop lda letters,x
cmp messtmp
beq ahead
inx
cpx #26
bne loop
ahead txa ;we got a match
clc
adc key
cmp #26
bcc nowrap
sbc #26
nowrap
tax
lda letters,x
space sta encrypted,y
iny
cpy messagelen
bne ploop
done
rts
.bend
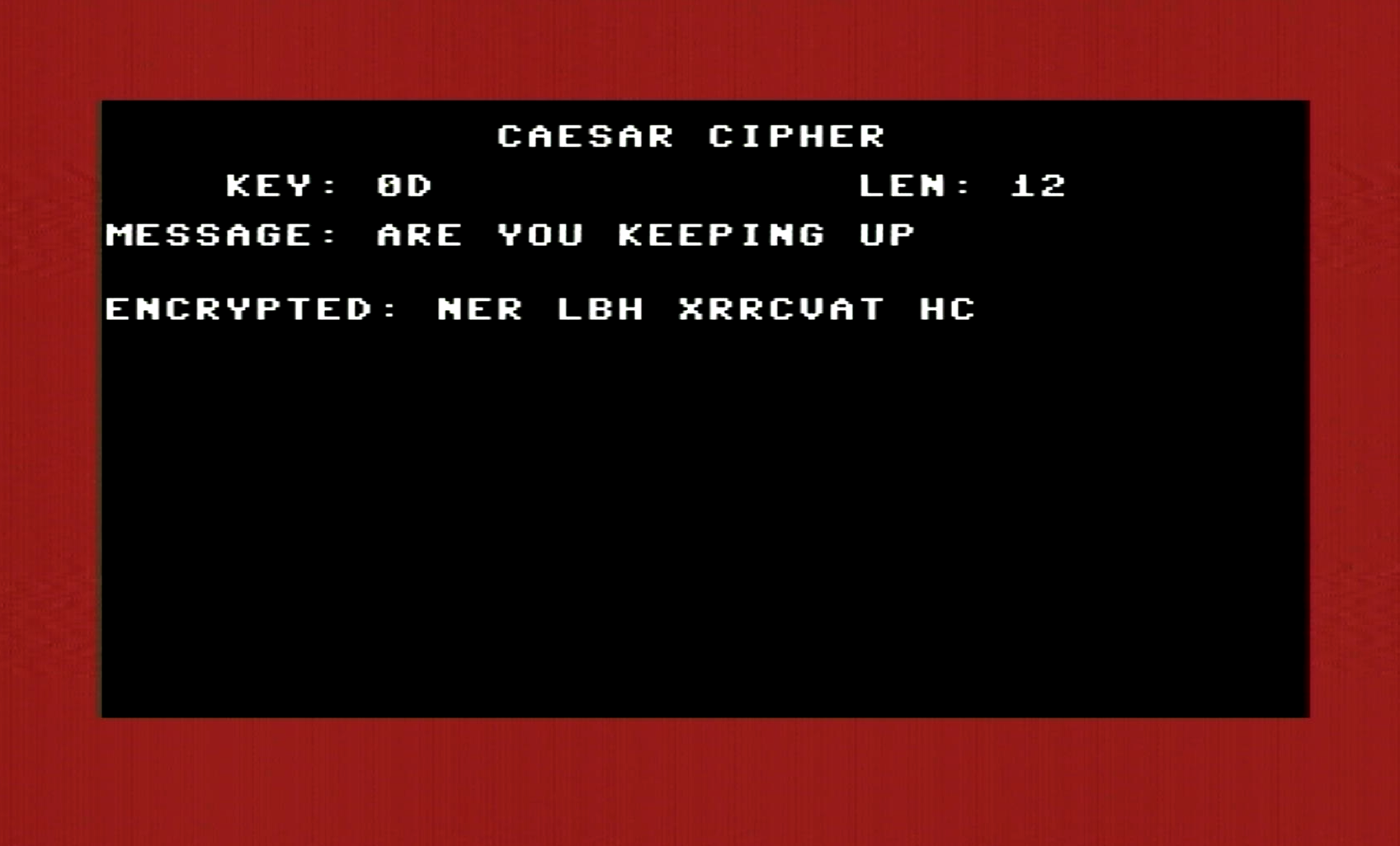
Great, it works!
Crack the code
Thanks to our blabbermouth target, cracking the Caesar cipher should be pretty easy with 1 Mhz processor. Let’s try all 26 possible combinations and see if we can figure it out.
We’ll use the same encrypt routine from above and cycle through all 26 key combinations and print them as two columns.

A fair amount of this code is here to handle printing in two columns. My first iteration of this printed 13 of the guesses in a single column and then waited for a keypress to do the second half of them. The Commodore doesn’t have a way for you to scroll back up, so you have to handle this some way.
chrout = $ffd2
plot = $fff0
screen = $0400
messtmp = $fb
encryptmp = $fd
messagelen = $fc
key .byte 0
message .null "ner lbh xrrcvat hc"
encrypted .null " "
row .byte 9 ; lay them out so they fit
col .byte 1 ; on a Commodore screen without scrolling
decryptloop
.block
ldx #26
stx key
loop
ldx row
ldy col
clc
jsr plot
ldx key
cpx #14
beq col2
doenc jsr dodecrypt
ldy #>encrypted
lda #<encrypted
jsr $ab1e
ldx key
inc row
dex
stx key
bne loop
rts
col2
lda #21
sta col
lda #8
sta row
jmp doenc
.bend
doecrypt
.block
ldy #0
ploop lda message,y
cmp #32
beq space ;skip ahead if it's a space
sta messtmp
ldx #0
loop lda letters,x
cmp messtmp
beq ahead
inx
cpx #26
bne loop
ahead txa ;we got a match
clc
adc key
cmp #26
bcc nowrap
sbc #26
nowrap
tax
lda letters,x
space sta encrypted,y
iny
cpy messagelen
bne ploop
done
rts
.bend
We’re wasting quite a few compute cycles jumping around and printing to the screen; something to keep in mind later in the series when we need to do millions of calculations .
Remember that I kept the message short here so that we could fit all 26 possible combinations in our implementation on one screen. A longer message will work just fine, but it’s not going to fit this nicely on the screen.
That’s it! We successfully “cracked’ our first message.
Next time we’ll tackle the PIN cracker from Terminator 2.
Extra credit:
- Add numbers and lowercase characters to the possible symbols a-z and 0-9. Maybe even some punctuation.
- Do the message cracking routine in python, maybe adding a switch flag to ask the user if you want to encrypt or decrypt